三维空间的位姿描述
介绍了四种姿态表示方式:旋转矩阵、欧拉角、轴角 和 四元数,以及它们之间相互转换关系的推导
位置描述
对欧氏三维空间中世界坐标系 \(\{O\}\) 下一点 \(P\),可用 \(^OP=\begin{pmatrix}p_x\\p_y\\p_z\end{pmatrix}\),描述其位置
姿态描述
旋转矩阵 Rotation Matrices
对于物体坐标系 \(\{O\}\) 下三个主轴的单位矢量 \(\hat X_O\)、\(\hat Y_O\) 和 \(\hat Z_O\) 在世界坐标系 \(\{W\}\) 上的投影 \(^W\hat X_O\)、\(^W\hat Y_O\) 和 \(^W\hat Z_O\),可以利用旋转矩阵 \(^W_OR\) 来表示物体坐标系的姿态
\[
\begin{aligned}
^W_OR = \begin{pmatrix}^W\hat X_O & ^W\hat Y_O & ^W\hat Z_O\end{pmatrix} =
\begin{pmatrix}
\hat X_O \cdot \hat X_W & \hat Y_O\cdot\hat X_W & \hat Z_O\cdot\hat X_W \\
\hat X_O \cdot \hat Y_W & \hat Y_O\cdot\hat Y_W & \hat Z_O\cdot\hat Y_W \\
\hat X_O \cdot \hat Z_W & \hat Y_O\cdot\hat Z_W & \hat Z_O\cdot\hat Z_W \\
\end{pmatrix}
= \begin{pmatrix}^O\hat X_W^T \\ ^O\hat Y_W^T \\ ^O\hat Z_W^T\end{pmatrix}
\end{aligned}
\]
显然,这是一个正交矩阵
\[
\begin{aligned}
^W_OR^T\ ^W_OR =
\begin{pmatrix}^W\hat X_O^T \\ ^W\hat Y_O^T \\ ^W\hat Z_O^T\end{pmatrix}
\begin{pmatrix}^W\hat X_O & ^W\hat Y_O & ^W\hat Z_O\end{pmatrix} = I_3
\end{aligned}
\]
进一步,由于旋转矩阵的所有行向量的模长均为1,且行向量之间两两正交,有 \(\det(R)=1\)
更普遍地,我们用 \(R = \begin{pmatrix}r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{pmatrix}\) 来表示一个旋转矩阵
接下来我们推导绕任一轴旋转的旋转矩阵的表达形式
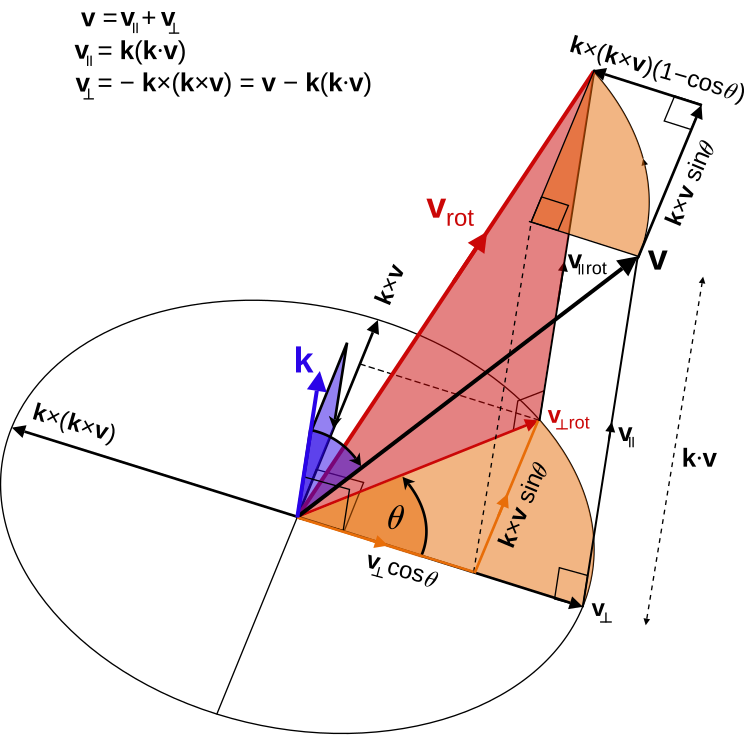
记三维空间中一任意向量 \(\bf v\) 绕旋转轴 \(\bf n=\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}\) 旋转 \(\theta\) 得到新向量 \(\bf v_{rot}\),其中 \(\bf n\) 为单位向量,\(n_x^2+n_y^2+n_z^2=1\)
则 \(\bf v\) 可以根据平行和正交于 \(\bf n\) 分为两部分 \(\bf v_\parallel\) 和 \(\bf v_\perp\),满足 \(\bf v=\bf v_\parallel+\bf v_\perp\)
其中
\[
\begin{cases}
\bf v_\parallel = (\bf v\cdot\bf n)n \\
\bf v_\perp = \bf v-(\bf v\cdot\bf n)n = -\bf n\times(\bf n\times\bf v)
\end{cases}
\]
而
\[
\begin{aligned}
\bf v_{rot} &= \bf v_{\parallel rot} + \bf v_{\perp rot} \\
&= \bf v_\parallel + \cos\theta\bf v_\perp + \sin\theta\bf n\times\bf v_\perp \\
&= (\bf v\cdot\bf n)n + \cos\theta\bf v_\perp + \sin\theta\bf n\times\bf v \\
&= \cos\theta\bf v+(1-\cos\theta)(\bf n\cdot\bf v)\bf n + \sin\theta\bf n\times\bf v
\end{aligned}
\]
上式就是 罗德里格斯旋转公式 Rodrigues' Rotation Formula,进一步我们令 \(\bf v\) 分别为 \(\begin{pmatrix}1&0&0\end{pmatrix}^T\),\(\begin{pmatrix}0&1&0\end{pmatrix}^T\) 和 \(\begin{pmatrix}0&0&1\end{pmatrix}^T\)
解得
\[
\begin{aligned}
\bf v_{rot} &= \cos\theta\begin{pmatrix}1\\0\\0\end{pmatrix}+(1-\cos\theta)\cdot n_x\begin{pmatrix}n_x\\n_y\\n_z\end{pmatrix}+\sin\theta\begin{pmatrix}0\\n_z\\-n_y\end{pmatrix} \\
&=\begin{pmatrix}(1-\cos\theta)n_x^2+\cos\theta\\(1-\cos\theta)n_xn_y+\sin\theta n_z\\(1-\cos\theta)n_xn_z-\sin\theta n_y\end{pmatrix}
\end{aligned}
\]
\[
\bf v_{rot}=\begin{pmatrix}(1-\cos\theta)n_yn_x-\sin\theta n_z\\(1-\cos\theta)n_y^2+\cos\theta\\(1-\cos\theta)n_yn_z+\sin\theta n_x\end{pmatrix}
\]
\[
\bf v_{rot}=\begin{pmatrix}(1-\cos\theta)n_zn_x+\sin\theta n_y\\(1-\cos\theta)n_zn_y-\sin\theta n_x\\(1-\cos\theta)n_z^2+\cos\theta\end{pmatrix}
\]
综上得到绕任意轴的旋转矩阵
\[
R=\begin{pmatrix}n_x^2(1-\cos\theta)+\cos\theta & n_xn_y(1-\cos\theta)-n_z\sin\theta & n_xn_z(1-\cos\theta)+n_y\sin\theta \\ n_yn_x(1-\cos\theta)+n_z\sin\theta & n_y^2(1-\cos\theta)+\cos\theta & n_yn_z(1-\cos\theta)-n_x\sin\theta \\ n_zn_x(1-\cos\theta)-n_y\sin\theta & n_zn_y(1-\cos\theta)+n_x\sin\theta & n_z^2(1-\cos\theta)+\cos\theta\end{pmatrix}
\]
欧拉角 Euler Angles
定义:
- 顺规:合法的欧拉角组中,任何两个连续的旋转,必须绕着不同的转动轴旋转,因此一共有12种顺规,被划分为两大类:
- 经典欧拉角 Proper Euler Angles:
zxz, xyx, yzy, zyz, xzx, yxy
- 泰特-布莱恩角 Tait-Bryan Angles:
xyz, yzx, zxy, xzy, zyx, yxz 其中按zyx顺序旋转的情况又被称为RPY角或XYZ固定角
- 内外旋:根据绕旋转后的新轴旋转还是绕世界坐标系中固定不动的轴旋转,欧拉角被分为内旋和外旋:
- 内旋 Intrisic Rotation, 又称为动态旋转,绕物体坐标系旋转
- 外旋 Extrinsic Rotation, 又称为静态旋转,绕世界坐标系旋转
- 内旋与外旋具有等价性
欧拉角 2 旋转矩阵
\[
\begin{aligned}
R &= R_Z(\gamma)R_Y(\beta)R_X(\alpha)=
\begin{pmatrix}
\cos\gamma & -\sin\gamma & 0 \\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta \\
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha \\
\end{pmatrix}
\\ \\
&=R_X^{-1}(\gamma)R_Y^{-1}(\beta)R_Z^{-1}(\alpha)=
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & \sin\alpha \\
0 & -\sin\alpha & \cos\alpha \\
\end{pmatrix}
\begin{pmatrix}
\cos\beta & 0 & -\sin\beta \\
0 & 1 & 0 \\
\sin\beta & 0 & \cos\beta \\
\end{pmatrix}
\begin{pmatrix}
\cos\gamma & \sin\gamma & 0 \\
-\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\end{aligned}
\]
旋转矩阵 2 欧拉角
以旋转顺序为 zyx 的内旋欧拉角为例
\[
\begin{aligned}
R = R_Z(\gamma)R_Y(\beta)R_X(\alpha) &=
\begin{pmatrix}
\cos\gamma & -\sin\gamma & 0 \\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta \\
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha \\
\end{pmatrix}
\\ \\&=
\begin{pmatrix}
\cos\gamma\cos\beta & -\sin\gamma\cos\alpha+\cos\gamma\sin\beta\sin\alpha & \sin\gamma\sin\alpha+\cos\gamma\sin\beta\cos\alpha \\
\sin\gamma\cos\beta & \cos\gamma\cos\alpha+\sin\gamma\sin\beta\sin\alpha & -\cos\gamma\sin\alpha+\sin\gamma\sin\beta\cos\alpha \\
-\sin\beta & \cos\beta\sin\alpha & \cos\beta\cos\alpha
\end{pmatrix}
\end{aligned}
\]
由此
\[
\begin{cases}
\alpha = \arctan(\frac{r_{32}}{r_{33}}) \\
\beta = \arcsin(-r_{31}) \\
\gamma = \arctan(\frac{r_{21}}{r_{11}}) \\
\end{cases}
\]
但当 \(\beta=\frac\pi2\) 时,\(R=\begin{pmatrix}0&-\sin(\gamma-\alpha)&cos(\gamma-\alpha)\\0&\cos(\gamma-\alpha)&\sin(\gamma-\alpha)\\1&0&0\end{pmatrix}\),旋转矩阵退化,无法解出唯一 \(\gamma\) 和\(\alpha\),这种情况被称为 奇异性 Singularity 或 万向节死锁 Glimbal Lock,可以被视为三维空间的物体姿态无法通过三个实数进行完全表达。在实践中,可以预分析机械最难出现的姿态,并通过有意地设计欧拉角顺规,尽可能避免出现万向节死锁的情况。
轴角 Axis Angle
轴角通过两个参数描述一个旋转:一条轴和描述绕这个轴的旋转量的角度,记为 \(<axis,angle>=\begin{pmatrix}\left[a_x\\a_y\\a_z\right]^T,\theta\end{pmatrix}\)
轴角 2 旋转矩阵
由罗德里格斯旋转公式可推出绕任意轴旋转的旋转矩阵,具体推导见 旋转矩阵 Rotation Matrix
\[
R=\begin{pmatrix}a_x^2(1-\cos\theta)+\cos\theta & a_xa_y(1-\cos\theta)-a_z\sin\theta & a_xa_z(1-\cos\theta)+a_y\sin\theta \\ a_ya_x(1-\cos\theta)+a_z\sin\theta & a_y^2(1-\cos\theta)+\cos\theta & a_ya_z(1-\cos\theta)-a_x\sin\theta \\ a_za_x(1-\cos\theta)-a_y\sin\theta & a_za_y(1-\cos\theta)+a_x\sin\theta & a_z^2(1-\cos\theta)+\cos\theta\end{pmatrix}
\]
旋转矩阵 2 轴角
观察上式,对给定旋转矩阵,有
\[
\begin{cases}
\theta = \arccos(\frac12(r_{11}+r_{22}+r_{33}-1)) \\
a_x = \frac{r_{32}-r_{23}}{\sqrt{(r_{32}-r_{23})^2+(r_{13}-r_{31})^2+(r_{21}-r_{12})^2}} \\
a_y = \frac{r_{13}-r_{31}}{\sqrt{(r_{32}-r_{23})^2+(r_{13}-r_{31})^2+(r_{21}-r_{12})^2}} \\
a_z = \frac{r_{21}-r_{12}}{\sqrt{(r_{32}-r_{23})^2+(r_{13}-r_{31})^2+(r_{21}-r_{12})^2}} \\
\end{cases}
\]
欧拉角 2 轴角
愉快地,我们可以利用 欧拉角 --> 四元数 --> 轴角 的方式得到
\[
\begin{cases}
\theta=2*\arccos(\cos\gamma\cos\beta\cos\alpha-\sin\gamma\sin\beta\sin\alpha) \\
a_x=\sin\gamma\sin\beta\cos\alpha+\cos\gamma\cos\beta\sin
\alpha\\
a_y=\sin\gamma\cos\beta\cos\alpha+\cos\gamma\sin\beta\sin\alpha\\
a_z=\cos\gamma\sin\beta\cos\alpha-\sin\gamma\cos\beta\sin\alpha
\end{cases}
\]
轴角 2 欧拉角
直接从轴角转为欧拉角比较困难,我们可以利用 轴角 --> 旋转矩阵 --> 欧拉角 的间接转化方式减少计算难度
\[
\begin{cases}
\alpha = \arctan(\frac{a_ya_z(1-\cos\theta)-a_x\sin\theta}{a_z^2(1-\cos\theta)+\cos\theta}) \\
\beta = \arcsin(a_y\sin\theta-a_xa_z(1-\cos\theta)) \\
\gamma = \arctan(\frac{a_xa_y(1-\cos\theta)-a_z\sin\theta}{a_x^2(1-\cos\theta)+\cos\theta}) \\
\end{cases}
\]
使用欧拉角进行表示时,某些情况会出现万向节锁和奇异的现象,需要特殊处理
四元数 Quaterions
不妨记四元数为 \(q=w+xi+yj+zk\),其中 \(i^2=j^2=k^2=ijk=-1\),而单位四元数满足 \(w^2+x^2+y^2+z^2=1\)
绕任意轴 \(n\) 旋转 \(\theta\) 的四元数,表示为 \(q=[w,x,y,z]=[\cos\frac\theta2,\sin\frac\theta2n_x,\sin\frac\theta2n_y,\sin\frac\theta2n_z]\)
轴角 2 四元数
\[
\begin{cases}
w = \cos\frac\theta2 \\
x = a_x\sin\frac\theta2 \\
y = a_y\sin\frac\theta2 \\
z = a_z\sin\frac\theta2 \\
\end{cases}
\]
四元数 2 轴角
\[
\begin{cases}
\theta = 2*\arccos(w)\\
a_x=\frac{x}{\sqrt{1-w^2}}\\
a_y=\frac{y}{\sqrt{1-w^2}}\\
a_z=\frac{z}{\sqrt{1-w^2}}\\
\end{cases}
\]
四元数 2 旋转矩阵
由罗德里格斯旋转公式可推出绕任意轴旋转的旋转矩阵,具体推导见 旋转矩阵 Rotation Matrix
\[
R=\begin{pmatrix}n_x^2(1-\cos\theta)+\cos\theta & n_xn_y(1-\cos\theta)-n_z\sin\theta & n_xn_z(1-\cos\theta)+n_y\sin\theta \\ n_yn_x(1-\cos\theta)+n_z\sin\theta & n_y^2(1-\cos\theta)+\cos\theta & n_yn_z(1-\cos\theta)-n_x\sin\theta \\ n_zn_x(1-\cos\theta)-n_y\sin\theta & n_zn_y(1-\cos\theta)+n_x\sin\theta & n_z^2(1-\cos\theta)+\cos\theta\end{pmatrix}
\]
将 \(n_x,n_y,n_z,\cos\theta,\sin\theta\) 用 \(w,x,y,z\) 表示
\[
\begin{cases}
\cos\theta = 1-2\cos^2\frac\theta2 \\
\sin\theta = 2\sin\frac\theta2\cos\frac\theta2
\end{cases}
\]
可以推出以下表达
\[
\begin{aligned}
R_q = \begin{pmatrix}
1-2y^2-2z^2 & 2xy-2wz & 2xz+2wy \\
2xy+2wz & 1-2x^2-2z^2 & 2yz-2wx \\
2xz-2wy & 2yz+2wx & 1-2x^2-2y^2 \\
\end{pmatrix}
\end{aligned}
\]
旋转矩阵 2 四元数
当给定旋转矩阵后,观察得到
\[
\begin{aligned}
r_{32}-r_{23}=(2yz+2wx)-(2yz-2wx)=4wx \\
r_{13}-r_{31}=(2xz+2wy)-(2xz-2wy)=4wy \\
r_{21}-r_{12}=(2xy+2wz)-(2xy-2wz)=4wz \\
\end{aligned}
\]
又有
\[
r_{11}+r_{22}+r_{33}=3-4x^2-4y^2-4z^2=4w^2-1
\]
进一步,可得
\[
\begin{cases}
w=\frac12\sqrt{1+r_{11}+r_{22}+r_{33}} \\
x=\frac{r_{32}-r_{23}}{4w} \\
y=\frac{r_{13}-r_{31}}{4w} \\
z=\frac{r_{21}-r_{12}}{4w} \\
\end{cases}
\]
欧拉角 2 四元数
对于欧拉角转四元数,我们可以根据四元数的定义写出以下表达
\[
\begin{aligned}
q(\gamma, \beta, \alpha) = q_z(\gamma)\ q_y(\beta)\ q_x(\alpha) =
\begin{pmatrix}
\cos\frac\gamma2 \\ 0 \\ 0 \\ \sin\frac\gamma2
\end{pmatrix}
\begin{pmatrix}
\cos\frac\beta2 \\ 0 \\ \sin\frac\beta2 \\ 0
\end{pmatrix}
\begin{pmatrix}
\cos\frac\alpha2 \\ \sin\frac\alpha2 \\ 0 \\ 0
\end{pmatrix} =
\begin{pmatrix}
\cos\frac\gamma2\cos\frac\beta2\cos\frac\alpha2 - \sin\frac\gamma2\sin\frac\beta2\sin\frac\alpha2 \\
\sin\frac\gamma2\sin\frac\beta2\cos\frac\alpha2 + \cos\frac\gamma2\cos\frac\beta2\sin\frac\alpha2 \\
\cos\frac\gamma2\sin\frac\beta2\cos\frac\alpha2 - \sin\frac\gamma2\cos\frac\beta2\sin\frac\alpha2 \\
\sin\frac\gamma2\cos\frac\beta2\cos\frac\alpha2 + \cos\frac\gamma2\sin\frac\beta2\sin\frac\alpha2 \\
\end{pmatrix}
\end{aligned}
\]
四元数 2 欧拉角
直接从四元数转为欧拉角比较困难,我们可以利用 四元数 --> 旋转矩阵 --> 欧拉角 的间接转化方式减少计算难度
\[
\begin{cases}
\alpha = \arctan(\frac{2yz+2wx}{1-2x^2-2y^2}) \\
\beta = \arcsin(2wy-2xz) \\
\gamma = \arctan(\frac{2xy+2wz}{1-2y^2-2z^2}) \\
\end{cases}
\]
同样地,使用欧拉角进行表示,某些情况会出现万向节锁和奇异的现象,需要特殊处理
各种表示方法对比
|
旋转矩阵 Rotation Matrix |
欧拉角 Euler Angles |
轴角 Axis Angle |
四元数 Quarternions |
| 优 |
可以表示三维空间任一姿态,并推广到 n 维空间 |
符合直觉 |
解决了万向锁 |
可以平滑插值,无万向节锁现象(本质是从四维空间描述三维姿态) |
| 劣 |
三维空间的姿态却用了九个量进行表示,存储冗余 |
奇异和万向节锁现象无法克服,无法平滑插值 |
无法平滑插值(本质是三维的) |
只对三维空间有效 |
参考资料
[1] @hideonInternet. 欧式空间的旋转表示[EB/OL]. https://hideoninternet.github.io/
categories/%E4%B8%89%E7%BB%B4%E5%9F%BA%E7%A1%80/%E6%97%8B%E8%BD%AC%E8%A1%A8%E5%BE%81/.
[2] 鸡哥. 三维旋转:欧拉角、四元数、旋转矩阵、轴角之间的转换[EB/OL]. https://zhuanlan.zhihu.com/p/45404840.
[3] XXX已失联. 四元数与欧拉角(RPY角)的相互转换[EB/OL]. https://www.cnblogs.com/21207-iHome/p/6894128.html.
[4] 展翅飞翔mxq. 姿态的三种描述方式——欧拉角、轴角、四元数[EB/OL]. https://blog.csdn.net/qq_21834027/article/details/85144454.
[5] John J. Craig. Introduction to Robotics: Mechanics and Control[M]. 3rd edition. Pearson, 2004.
[6] Martin John Baker. Maths - Rotation conversions[EB/OL]. https://www.euclideanspace.com/maths/geometry/rotations/conversions/index.htm.
[7] li chongbin. 三维空间绕任意轴旋转矩阵的推导[EB/OL]. https://zhuanlan.zhihu.com/p/56587491.
[8] wtyuan. 罗德里格斯旋转公式(Rodrigues’ rotation formula)推导[EB/OL]. https://www.cnblogs.com/wtyuan/p/12324495.html.
[9] Maschen. File:Orthogonal decomposition unit vector rodrigues rotation formula.svg[R]. 2015.
[10] 罗伯特祥. 四元数笔记(3)—— 轴角表示法与四元数表示的区别[EB/OL]. https://blog.csdn.net/weixin_43455581/article/details/108413001.