Trajectory Tracking Task based on Nonlinear Model Prediction and PHR Augmented Lagrange Method
Kinematic Model
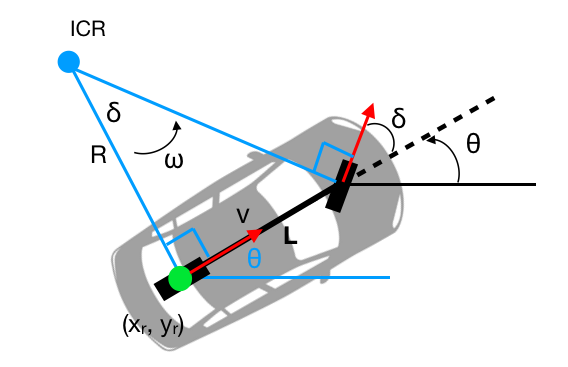
| Variables | Descriptions | Variables | Descriptions |
|---|---|---|---|
| \([x_r,y_r]\) | position of rear wheel | \(v\) | velocity at rear wheel |
| \(\theta\) | vehicle orientation | \(a\) | acceleration input |
| \(L\) | vehicle length | \(\delta\) | steering input |
So that, I use below equation to update states in discrete time domain, which is
Loss Function
Define the \(k\)-th control point's loss function as below:
And there are physical limits
PHR ALM
We can rewrite the problem to a general form
Denote \({\mathbf u}_k=\begin{pmatrix}u_{k+1}\\ u_{k+2}\\\vdots\\ u_{k+N+1}\end{pmatrix}\in{\rm R}^{2N}\)
Ant then
Which
Where \(\rho>0, \mu\succeq0\)
We update the variables and parameters in a loop
In this particular case, we don't have equality constraints. Just simply ignore \(h({\mathbf u}_k)\) and \(\lambda\)
Demo Code
You can get the full code via https://github.com/ZhangzrJerry/Introduction-to-Mobile-Robotics/demo4_mpc_alm
import numpy as np
import matplotlib.pyplot as plt
import math
import cv2
import os
import imageio
from tqdm import tqdm
# function for render dots via cubic spline
def draw(dots, color, linestyle, file_dir, idx):
n = len(dots) - 1
t1 = np.reshape(np.linspace(0, 1, 1001), [1, 1001])
t2 = t1 ** 2
t3 = t1 ** 3
t0 = np.reshape([1 for _ in range(1001)], [1, 1001])
tmp = np.zeros((n, n + 1))
tmp[0, 0] = 2
tmp[0, 1] = -3
tmp[0, 2] = 1
for i in range(1,n-1):
tmp[i, i] = 1
tmp[i, i+1] = -2
tmp[i, i+2] = 1
tmp[-1, -1] = -1
tmp[-1, -2] = 1
A = tmp.dot(dots)
tmp = np.zeros((n, n + 1))
tmp[0, 0] = -3
tmp[0, 1] = 4
tmp[0, 2]= -1
for i in range(1,n-1):
tmp[i, i] = -1
tmp[i, i+1] = 2
tmp[i, i+2] = -1
tmp[-1, -1] = 1
tmp[-1, -2] = -1
B = tmp.dot(dots)
tmp = np.zeros((n, n + 1))
for i in range(1, n):
tmp[i, i] = -1
tmp[i, i+1] = 1
C = tmp.dot(dots)
tmp = np.zeros((n, n + 1))
for i in range(0, n):
tmp[i, i] = 1
D = tmp.dot(dots)
interval = np.array([])
for i in range(n):
if len(interval) == 0:
interval = np.reshape(A[i], [-1, 1]).dot(t3) + \
np.reshape(B[i], [-1, 1]).dot(t2) + \
np.reshape(C[i], [-1, 1]).dot(t1) + \
np.reshape(D[i], [-1, 1]).dot(t0)
else:
interval = np.append(interval, (
np.reshape(A[i], [-1, 1]).dot(t3) + \
np.reshape(B[i], [-1, 1]).dot(t2) + \
np.reshape(C[i], [-1, 1]).dot(t1) + \
np.reshape(D[i], [-1, 1]).dot(t0)
), axis=1)
plt.plot(interval[0], interval[1], color=color, linestyle=linestyle)
plt.scatter(dots.T[0], dots.T[1], color=color, s=8)
plt.gca().set_axis_off()
plt.gca().set_xbound(-3.5, 2*math.pi+3.5)
plt.gca().set_ybound(-6.5, 0.5)
plt.gca().set_aspect('equal', adjustable='box')
if idx > -1:
plt.savefig(file_dir + str(idx) + '.png')
plt.gca().cla()
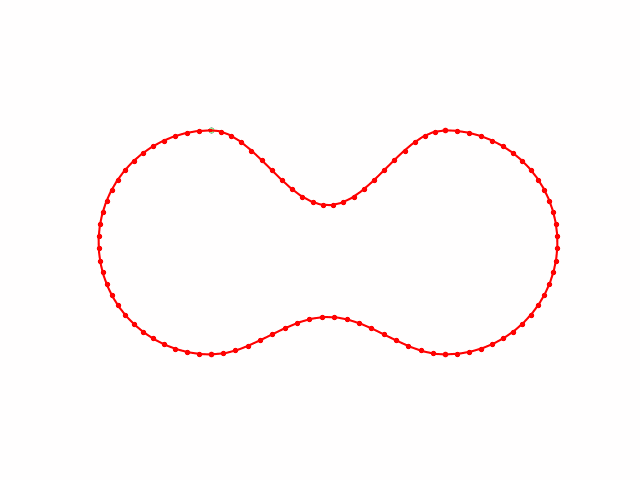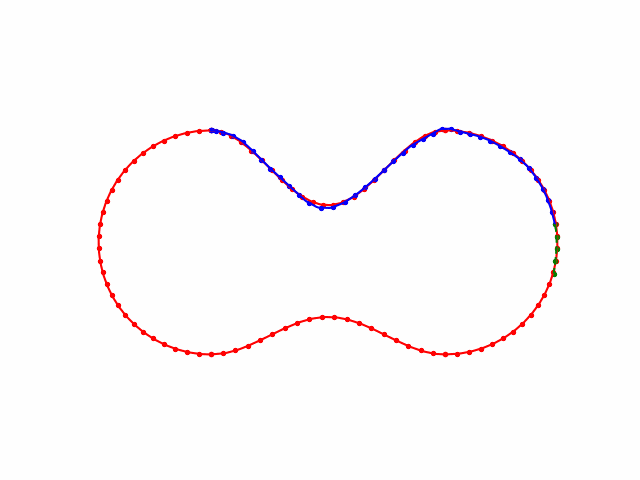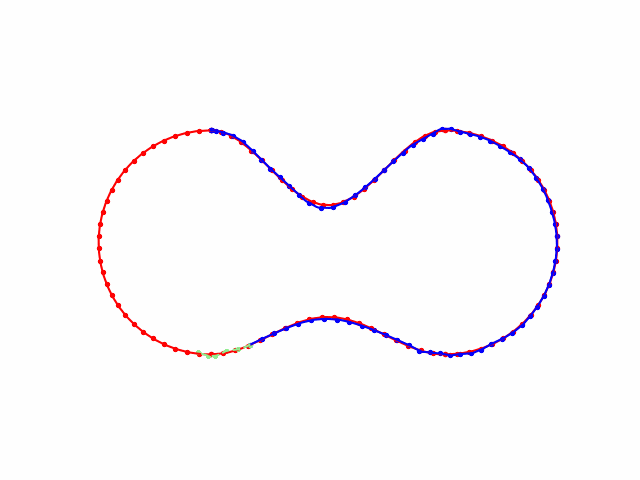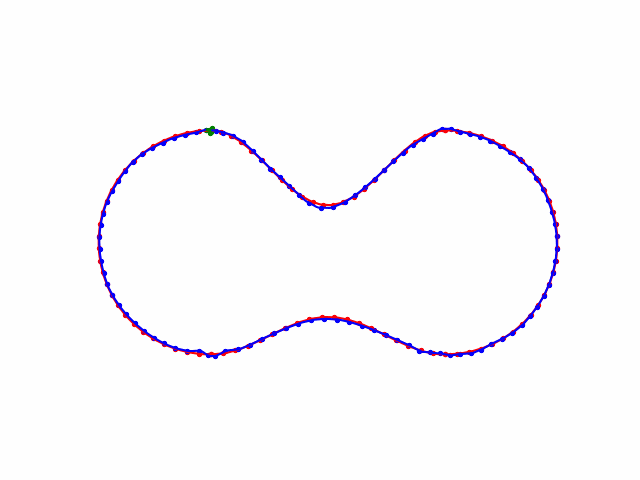
# define control points as below
# It's better to minimize the stretched energy when generating the control points.
# Here I just randomly pick some, so it may not give you a good enough performance.
# We need the wisdom of integration of plan and control [:doge:]
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 24)],
[[3*math.cos(_)+2*math.pi, 3*math.sin(_)-3] for _ in np.linspace(math.pi/2, -math.pi/2, 30)],
[[_, -0.5*math.cos(_) - 5.5] for _ in np.linspace(2 * math.pi, 0, 20)],
[[-3*math.cos(_), 3*math.sin(_)-3] for _ in np.linspace(-math.pi/2, math.pi/2, 30)]
])
# bicycle kinematic
def kinematic(prev_state, a, delta, n, dt, L):
state = np.zeros((n+1, 4))
state[0] = prev_state
for i in range(0, n):
state[i+1][3] = state[i][3] + a[i] * dt
state[i+1][2] = state[i][2] + (state[i][3] + state[i+1][3])/2 * delta[i] / L * dt
state[i+1][0] = state[i][0] + (state[i][3] * math.cos(state[i][2]) + state[i+1][3] * math.cos(state[i+1][2])) / 2 * dt
state[i+1][1] = state[i][1] + (state[i][3] * math.sin(state[i][2]) + state[i+1][3] * math.sin(state[i+1][2])) / 2 * dt
return state[1:]
# loss function that needs to minimize
def f(x, x_ref, y, y_ref, a, a_prev, delta, delta_prev, s_weight=10, a_weight=1, delta_weight=1):
return np.linalg.norm(x - x_ref) ** 2 * s_weight + \
np.linalg.norm(y - y_ref) ** 2 * s_weight + \
np.linalg.norm(a - a_prev) ** 2 * a_weight + \
np.linalg.norm(delta - delta_prev) ** 2 * delta_weight
# inequality constraint
def h(a, delta, v, a_min=-2, a_max=2, delta_min=-0.8, delta_max=0.8, v_min=-5, v_max=10):
return np.array([
a_min - a,
a - a_max,
delta_min - delta,
delta - delta_max,
v_min - v,
v - v_max
])
# PHR Augmented Lagrangian
def L(prev_state, x_ref, y_ref, a, a_prev, delta, delta_prev, rho, mu, tau, wheel_base, s_weight=10, a_weight=100, delta_weight=1):
x, y, phi, v = kinematic(prev_state, a, delta, len(a), tau, wheel_base).T
return f(x, x_ref, y, y_ref, a, a_prev, delta, delta_prev, s_weight, a_weight, delta_weight) + \
rho / 2 * (np.linalg.norm(np.maximum((h(a, delta, v) + mu / rho), 0)) ** 2)
# numerical gradient
def gradient(prev_state, x_ref, y_ref, a, a_prev, delta, delta_prev, rho, mu, tau, wheel_base, s_weight=10, a_weight=100, delta_weight=1):
epi = 1e-16
grad_a = np.zeros(a.shape)
for i in range(len(a)):
a_plus = np.copy(a)
a_plus[i] += epi
a_minus = np.copy(a)
a_minus[i] -= epi
grad_a[i] = (L(prev_state, x_ref, y_ref, a_plus, a_prev, delta, delta_prev, rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight) - \
L(prev_state, x_ref, y_ref, a_minus, a_prev, delta, delta_prev, rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)) / (2 * epi)
grad_delta = np.zeros(delta.shape)
for i in range(len(delta)):
delta_plus = np.copy(delta)
delta_plus[i] += epi
delta_minus = np.copy(delta)
delta_minus[i] -= epi
grad_delta[i] = (L(prev_state, x_ref, y_ref, a, a_prev, delta_plus, delta_prev, rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight) - \
L(prev_state, x_ref, y_ref, a, a_prev, delta_minus, delta_prev, rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)) / (2 * epi)
return np.append(grad_a, grad_delta, axis=0)
# Hyperparameters
N = 5 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 150 # max iteration for a single point
s_weight = 1 # weight for control points
a_weight = 2 # weight for acceleration
delta_weight = 3 # weight for steering angle
prev_state = [0, 0, 0, 0] # x, y, phi, v
prev_input = [0, 0] # a, delta
wheel_base = 0.005 # wheel base
input = np.zeros(N * 2)
states = [
np.array(prev_state) for _ in range(3)
] # states, repeating stack for rendering better
inputs = [] # inputs
predict = 0
full_dir = 'output/full'
brief_dir = 'output/brief'
for idx in range(len(dots)):
# param
rho = 1
xi = 5e-1
mu = 1
# reference
x_ref = dots[idx:idx+N, 0]
y_ref = dots[idx:idx+N, 1]
n = len(x_ref)
while n < N:
x_ref = np.append(x_ref, x_ref[-1])
y_ref = np.append(y_ref, y_ref[-1])
n += 1
# PHR
for iter in range(max_iteration):
loss = L(prev_state, x_ref, y_ref, input[:n], np.append(prev_input[0], input[:n-1]), input[n:], np.append(prev_input[1], input[n:2 * n-1]), rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)
grad = gradient(prev_state, x_ref, y_ref, input[:n], np.append(prev_input[0], input[:n-1]), input[n:], np.append(prev_input[1], input[n:2 * n-1]), rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)
if predict % 20 == 0:
draw(dots, 'red', '-', '', -1)
draw(np.array(states), 'blue', '-', '' , -1)
draw(np.vstack([prev_state, kinematic(prev_state, input[:n], input[n:], n, tau, wheel_base)]), 'lightgreen', '--', full_dir, predict)
print((idx, iter, predict), loss)
predict += 1
# LBFGS
B = np.identity(n * 2)
last_grad = grad
last_loss = 0x3f3f3f3f
while np.linalg.norm(grad) > xi and last_loss - loss > xi:
direction = -B.dot(grad)
rbound = 0x3f3f3f3f if idx == 0 else 10
l, r, alpha = 0, rbound, 1
# Lewis-overton line search
for _ in range(1000):
new_input = input + alpha * direction
new_loss = L(prev_state, x_ref, y_ref, new_input[:n], np.append(prev_input[0], new_input[:n-1]), new_input[n:], np.append(prev_input[1], new_input[n:2 * n-1]), rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)
new_grad = gradient(prev_state, x_ref, y_ref, new_input[:n], np.append(prev_input[0], new_input[:n-1]), new_input[n:], np.append(prev_input[1], new_input[n:2 * n-1]), rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)
if loss < new_loss - 1e-4 * alpha * grad.dot(direction):
r = alpha
elif new_grad.dot(direction) < 0.95 * grad.dot(direction):
l = alpha
else:
break
if r < rbound:
alpha = (l + r) / 2
else:
alpha = 2 * l
# update parameters
delta_x = new_input - input
delta_g = gradient(prev_state, x_ref, y_ref, new_input[:n], np.append(prev_input[0], new_input[:n-1]), new_input[n:], np.append(prev_input[1], new_input[n:2 * n-1]), rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight) - grad
# cautious
if delta_g.T.dot(delta_x) > 1e-6 * np.linalg.norm(grad) * input.T.dot(input):
B = (np.identity(2*n)-delta_x.dot(delta_g.T) / delta_g.T.dot(delta_x)).dot(B).dot(np.identity(2*n)-delta_g.dot(delta_x.T) / delta_g.T.dot(delta_x)) + delta_x.dot(delta_x.T) / delta_g.T.dot(delta_x)
input = new_input
last_loss = loss
loss = L(prev_state, x_ref, y_ref, input[:n], np.append(prev_input[0], input[:n-1]), input[n:], np.append(prev_input[1], input[n:2 * n-1]), rho, mu, tau, wheel_base, s_weight, a_weight, delta_weight)
grad = grad + delta_g
# update PHR parameters
state = kinematic(prev_state, input[:n], input[n:], n, tau, wheel_base)
mu = np.max(np.maximum(mu + rho * h(input[:n], input[n:], state[:,3]), 0))
rho = np.minimum(rho * (1 + gamma), beta)
xi = min(min_xi,xi * 0.9)
# specific boundary
if loss < 5e-2 and iter > 5:
break
last_grad = grad
prev_input = [input[0], input[N]]
prev_state = state[0]
states.append(prev_state)
inputs.append(prev_input)
# initialize the input 0,1,...,n-2,n,n+1,2n-2
# with last input 1,2,...,n-1,n+1,n+2,...,2n-1
# rather than randomly assigned them to be 0
input[:N-1]=input[1:N]
input[N:2*N-1]=input[N+1:2*N]
input[N-1]=0
input[2*N-1]=0
# render and print
draw(dots, 'red', '-', '', -1)
draw(np.array(states), 'blue', '-', '' , -1)
draw(np.array(state), 'green', '--', brief_dir, idx)
draw(dots, 'red', '-', '', -1)
draw(np.array(states), 'blue', '-', '' , -1)
draw(np.array(state), 'green', '--', full_dir, predict)
predict += 1
print(idx, loss, grad.mean())
# generate animate
path = full_dir
fps = 120
files = [os.path.join(path, f) for f in os.listdir(path)]
files.sort(key=lambda x: int(os.path.splitext(os.path.basename(x))[0]))
frames = []
for f in tqdm(files):
img = imageio.imread(f) # RGB格式的array
img = cv2.resize(img, (640, 480)) # Resize to (640, 480)
frames.append(img)
imageio.mimsave(path+'.gif', frames, duration=1/fps)
Reference
[1] Z. Wang, “Numerical Optimization in Robotics.”
[2] Y. Ding, “Simple Understanding of Kinematic Bicycle Model.” [Online]. Available: https://www.shuffleai.blog/blog/Simple_Understanding_of_Kinematic_Bicycle_Model.html