非线性模型预测控制调参小记
\(A\)
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 24)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 12)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 10)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 5)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 15)]
])
dots = dots * 20
N = 8 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 15 # max iteration for a single point
a_weight = 0 # weight for acceleration
delta_weight = 0 # weight for steering angle
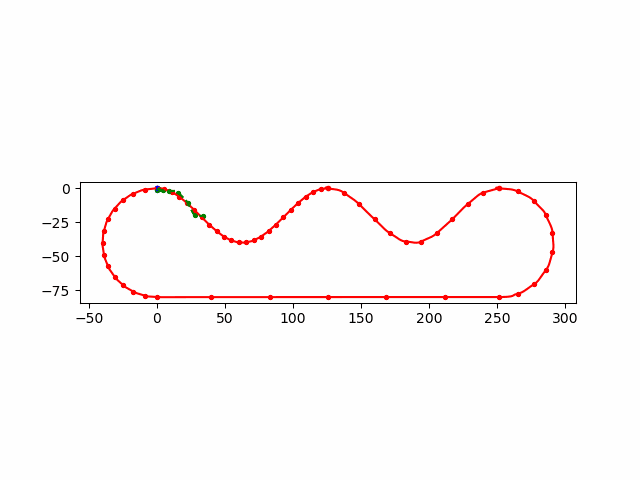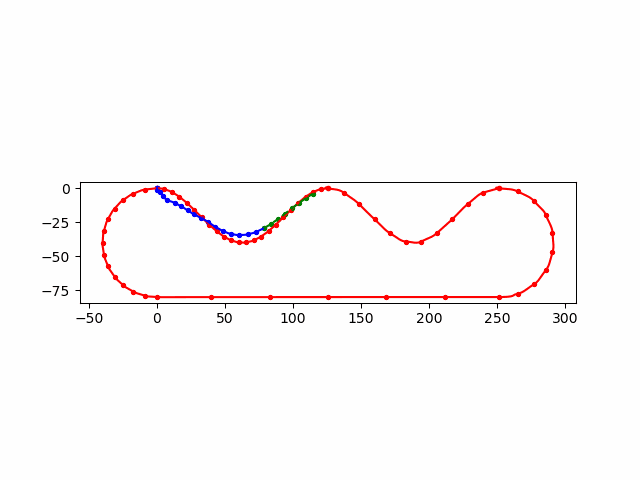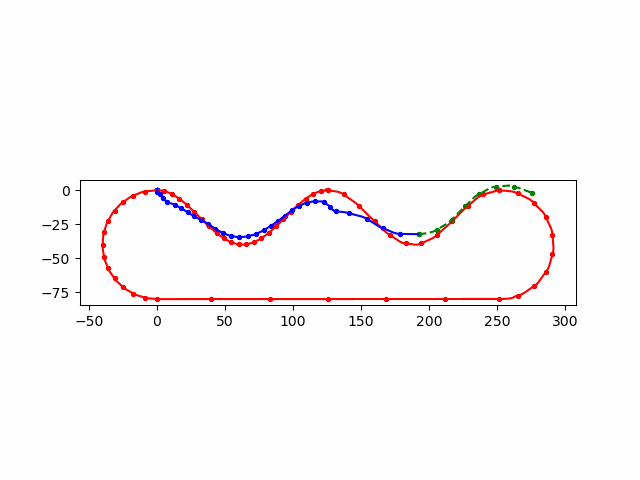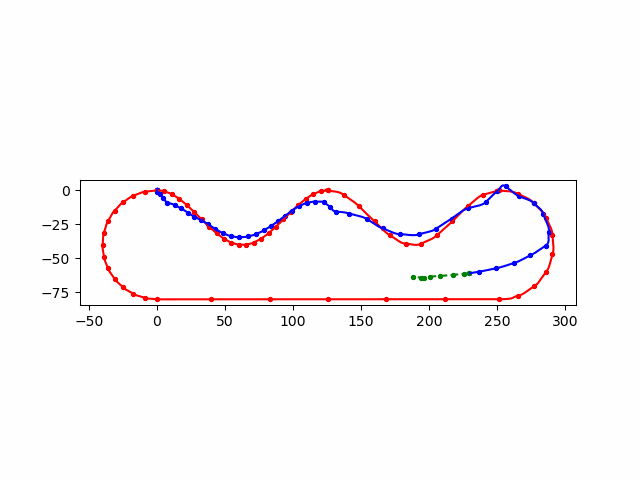
\(B\)
加入了 init_guess,每次 \(n\) 个输入,前 \(n-1\) 个来自上一次的优化后的结果
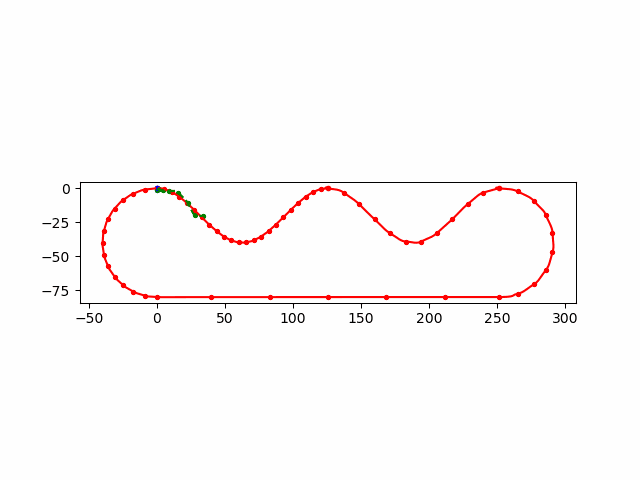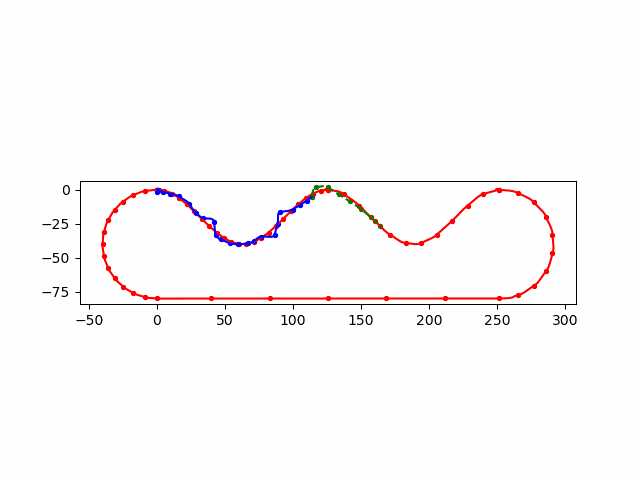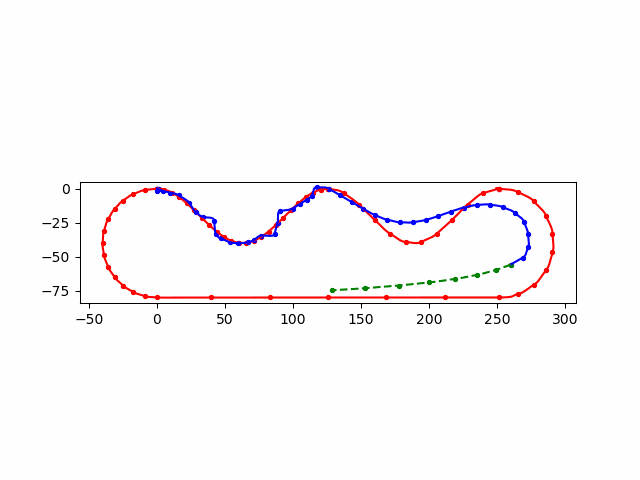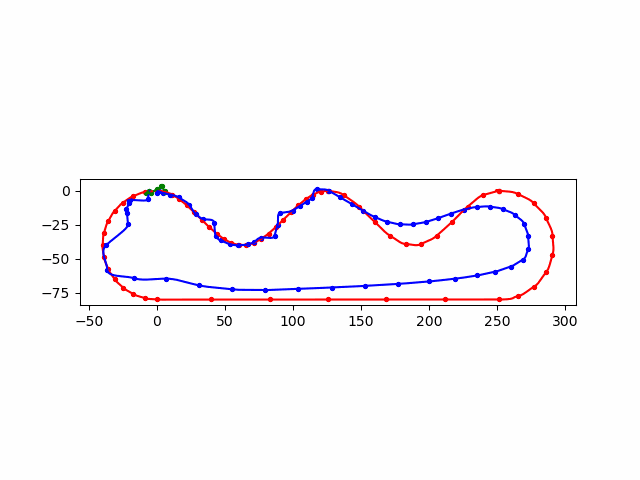
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 24)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 12)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 10)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 5)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 15)]
])
dots = dots * 20
N = 8 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 15 # max iteration for a single point
a_weight = 0 # weight for acceleration
delta_weight = 0 # weight for steering angle
\(\Gamma\)
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 24)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 12)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 10)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 5)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 15)]
])
dots = dots * 20
N = 3 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 25 # max iteration for a single point
a_weight = 5e-2 # weight for acceleration
delta_weight = 3e-1 # weight for steering angle
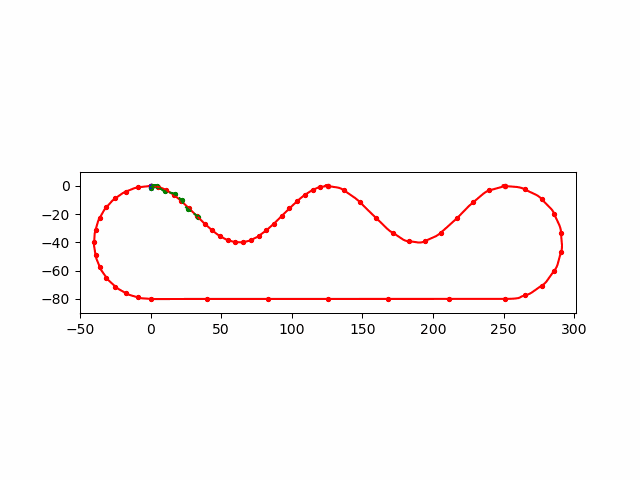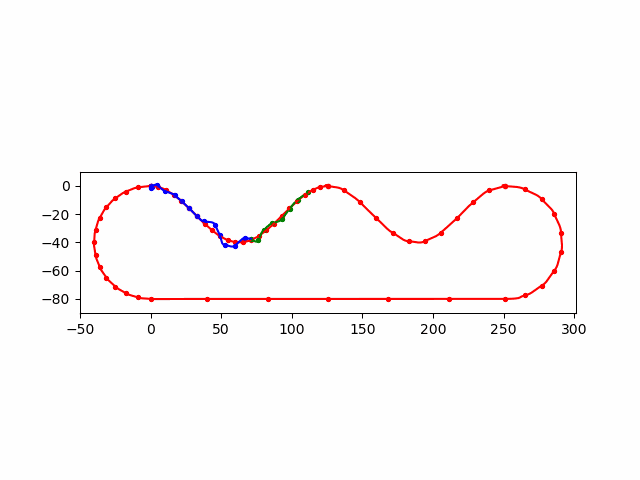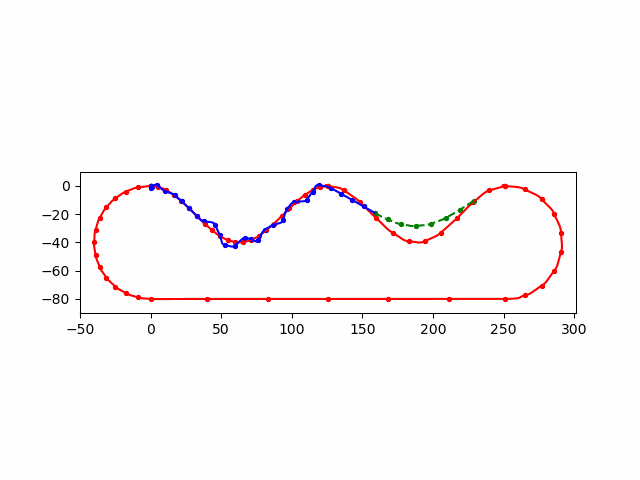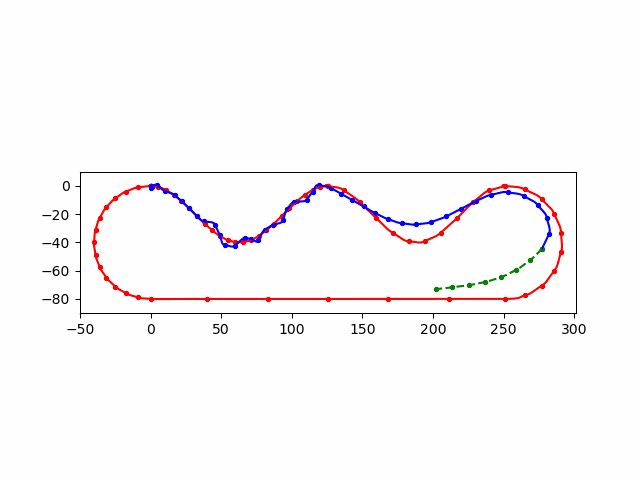
\(\Delta\)
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 48)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 24)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 20)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 10)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 30)]
])
dots = dots * 20
N = 4 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 25 # max iteration for a single point
a_weight = 5e-2 # weight for acceleration
delta_weight = 3e-1 # weight for steering angle
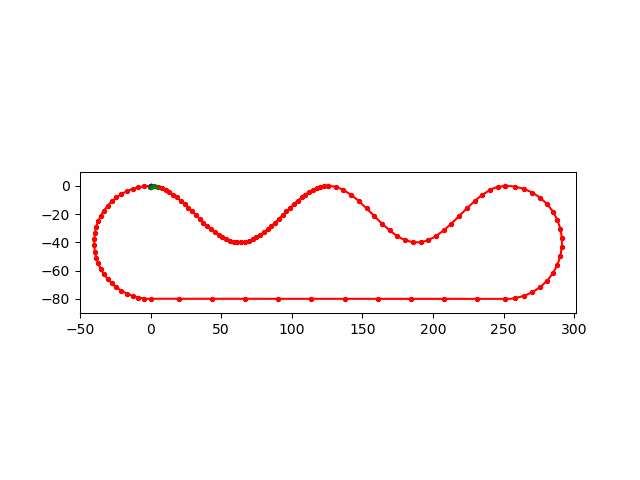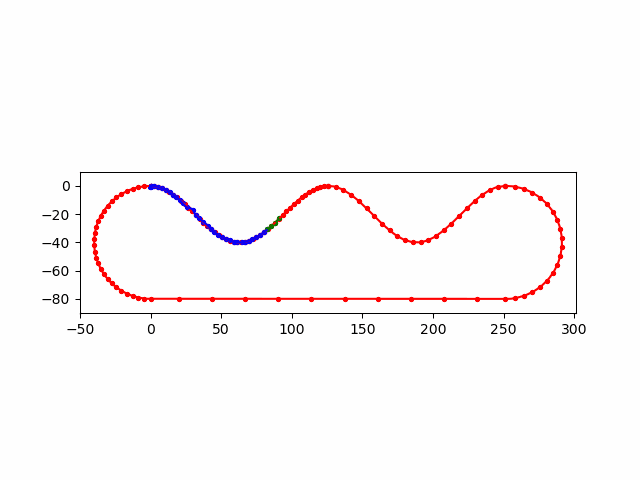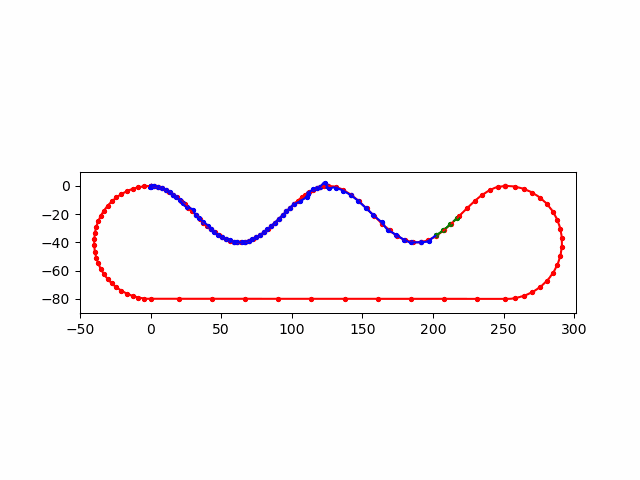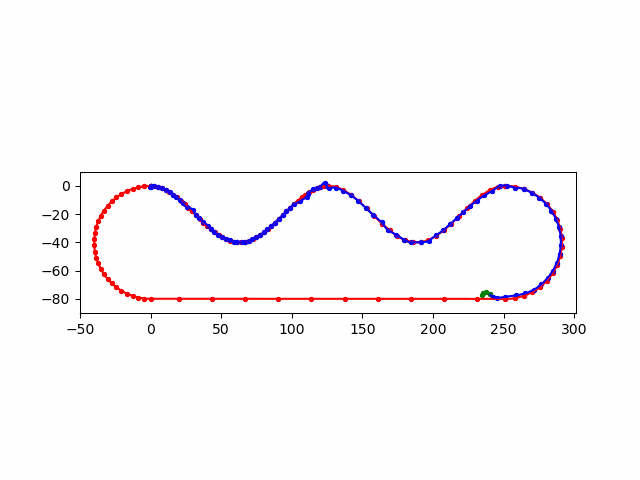
\(E\)
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 48)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 24)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 20)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 10)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 30)]
])
N = 4 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 25 # max iteration for a single point
a_weight = 5e-2 # weight for acceleration
delta_weight = 3e-1 # weight for steering angle

\(Z\)
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 48)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 24)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 20)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 10)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 30)]
])
N = 4 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 25 # max iteration for a single point
a_weight = 5e-2 # weight for acceleration
delta_weight = 3e-1 # weight for steering angle
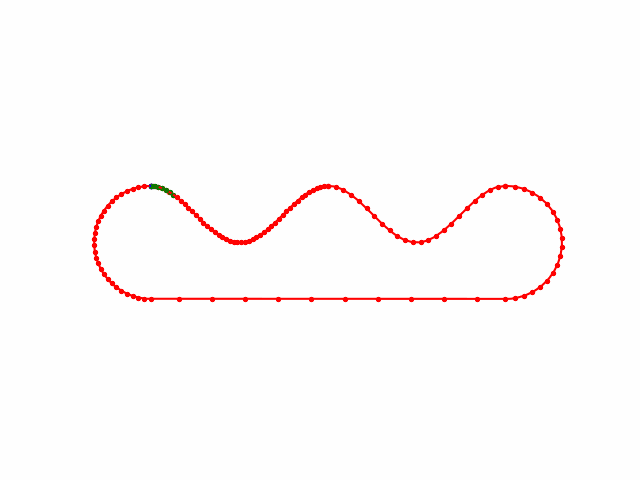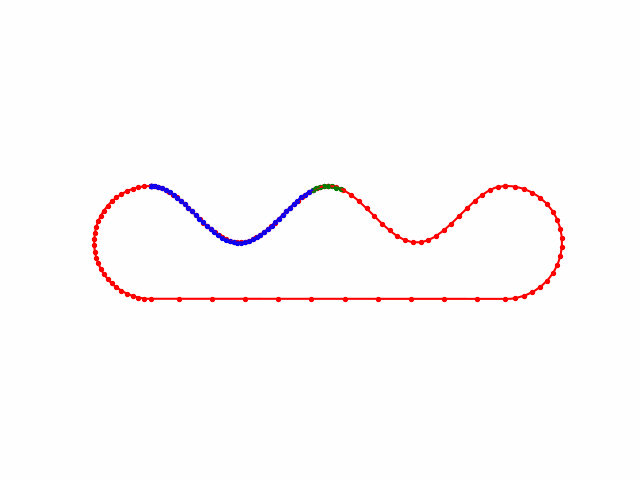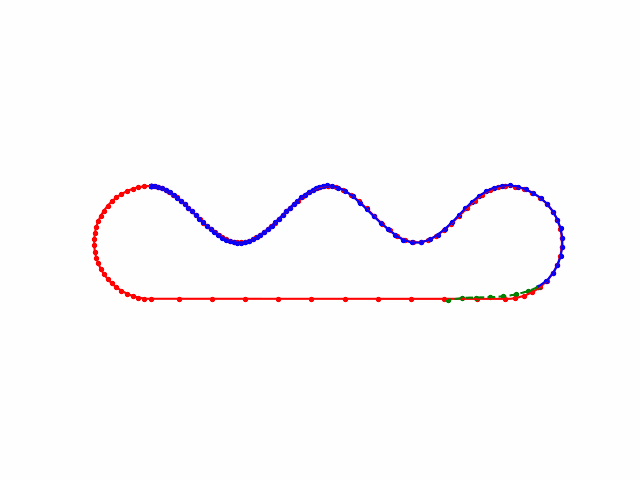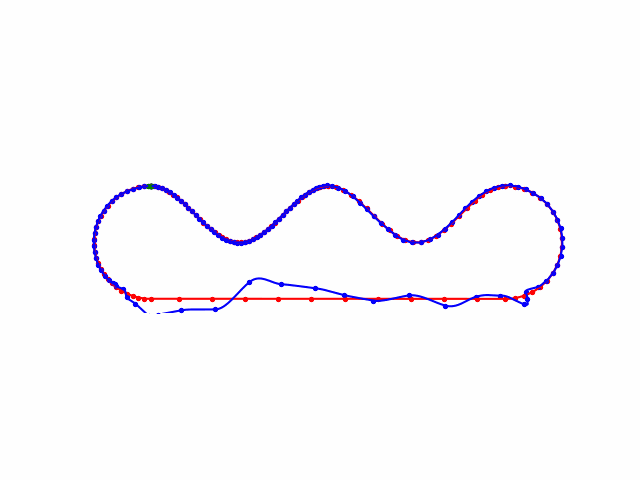
地图控制点随手生成的,没有做stretch energy优化,速度突变的太厉害
\(H\)
dots = np.vstack([
[[0, 0] for _ in range(1)],
[[_, math.cos(_) - 1] for _ in np.linspace(0, 2 * math.pi, 48)],
[[_, math.cos(_) - 1] for _ in np.linspace(2 * math.pi, 4 * math.pi, 24)],
[[2*math.cos(_)+4*math.pi, 2*math.sin(_)-2] for _ in np.linspace(math.pi/2, -math.pi/2, 20)],
[[_, -4] for _ in np.linspace(4*math.pi - 1, 1, 10)],
[[-2*math.cos(_), 2*math.sin(_)-2] for _ in np.linspace(-math.pi/2, math.pi/2, 30)]
])
N = 8 # predict step
tau = 1 # time constant
epsilon_cons = 1e-3 # constraint criterion
epsilon_prec = 1e-3 # precision criterion
min_xi = 1e-3 # min step precision
beta = 5000 # panalty upper bound
gamma = 5e-1 # penalty increase factor
max_iteration = 25 # max iteration for a single point
a_weight = 5e-2 # weight for acceleration
delta_weight = 3e-1 # weight for steering angle

\(\Theta\)
N=3

\(I\)
N=11

\(K\)
N=11
加入了一个参数,使前 n-1 个输入沿梯度方向走的时候比第 n 个输入沿梯度更新时,步长更小

\(\Lambda\)
N = 11
a_weight=3e-2

\(N\)
N = 8
a_weight = 5e-2 # weight for acceleration
delta_weight = 5e-1 # weight for steering angle

\(M\)
N = 8
a_weight = 5e-2 # weight for acceleration
delta_weight = 5e-1 # weight for steering angle

\(\Xi\)
a_weight = 2e-1 # weight for acceleration
delta_weight = 1e1 # weight for steering angle

\(O\)

\(\Pi\)
\(P\)

\(\Sigma\)
\(T\)

\(\Upsilon\)

\(\Phi\)
