ELEC 3200 Lab1 Report - Magnetic Levitation System
Mathematic Model
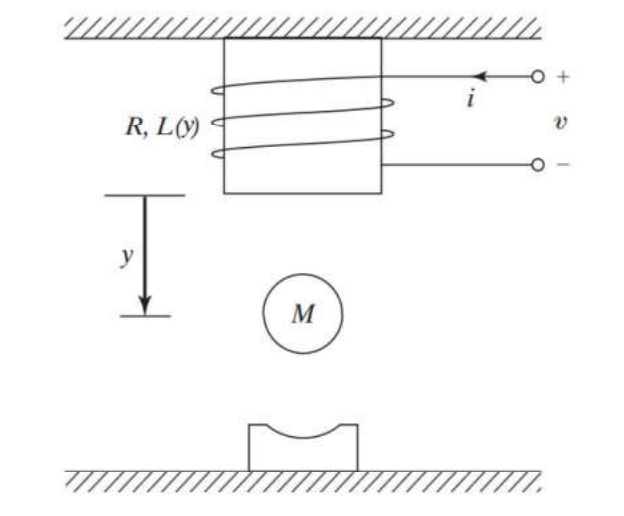
\[
\begin{aligned}
\left[\begin{matrix}
\dot x_1(t)\\\dot x_2(t)\\\dot x_3(t)
\end{matrix}\right]&=\left[\begin{matrix}
\frac{u(t)-Rx_1(t)+rL_1x_1(t)x_3(t)}{(L_0+\frac{rL_1}{x_2(t)})x_2^2(t)}\\
x_2(t)\\
-\frac{rL_1x_1^2(t)}{2Mx_2^2(t)}+g
\end{matrix}\right]\\
y(t)&=x_2(t)
\end{aligned}
\]
Then \(u_0=Ry_0\sqrt{\frac{2Mg}{rL_1}}\), \({\mathbf x}_0=\left[\begin{matrix}y_0\sqrt{\frac{2Mg}{rL_1}}&y_0&0\end{matrix}\right]^T\), \(y_0=y_0\)
\[
\begin{aligned}
{\dot {\tilde {\mathbf x}}}(t) &= \left[\begin{matrix}
-\frac R{L_0+\frac{rL_1}{y_0}} & 0 & \frac{\sqrt{2rL_1Mg}}{y_0(L_0+\frac{rL_1}{y_0})} \\
0 & 0 & 1\\
-\frac1{y_0}\sqrt{\frac{2rL_1g}{M}} & \frac{2g}{y_0} & 0
\end{matrix}\right]{\tilde{\mathbf x}}(t)+\left[\begin{matrix}
\frac1{L_0+\frac{rL_1}{y_0}} \\ 0 \\ 0
\end{matrix}\right]{\tilde u}(t) \\
{\tilde y}(t) &= \left[\begin{matrix} 0 & 1 & 0
\end{matrix}\right]{\tilde {\mathbf x}}(t)
\end{aligned}
\]
Numerical Model
| Param | Value |
|---|---|
| Coil Inductance \(L_0\) | \(0.272\ {\rm H}\) |
| Coil Resistance \(R\) | \(13.2\ \Omega\) |
| Ball Mass \(M\) | \(0.091\ {\rm Kg}\) |
| Coil Inductance Coefficient \(rL_1\) | \(2.66\times10^{-3}\) |
| Gravity Acceleration \(g\) | \(9.78495\ m/s^2\) |
| Initial Height \(y_0\) | \(0.1\ m\) |
\[
\begin{aligned}
{\dot {\tilde {\mathbf x}}}(t) &= \left[\begin{matrix}
-36.5989 & 0 & 6.6682\\
0 & 0 & 1.0000\\
-24.0499 &652.3300& 0\\
\end{matrix}\right]{\tilde{\mathbf x}}(t)+\left[\begin{matrix}
2.7726 \\ 0 \\ 0
\end{matrix}\right]{\tilde u}(t) \\
{\tilde y}(t) &= \left[\begin{matrix} 0& 1&0
\end{matrix}\right]{\tilde {\mathbf x}}(t)
\end{aligned}
\]
\[
G(s)=\frac{-66.68}{s^3+36.6s^2-492s-23870}
\]
MATLAB
Pole Placement & Controller Design
L0 = 2.72e-1;
R = 1.32e1;
M = 9.1e-2;
rL1 = 2.66e-3;
g = 9.78495e0;
y0 = 4e-2;
A = [-R/(L0+rL1/y0) 0 sqrt(2*rL1*M*g)/y0/(L0+rL1/y0);0 0 1; -1/y0*sqrt(2*rL1*g/M) 2*g/y0 0];
B = [1/(L0+rL1/y0); 0; 0];
C = [0 1 0];
D = [];
sys = ss(A, B, C, D);
sys_tf = tf(sys);
as = sys_tf.Denominator{1};
bs = sys_tf.Numerator{1};
syms s;
cs = reshape(flip(coeffs(expand((s+40)*(s+45-45i)*(s+45+45i)*(s+120-120i)*(s+120+120i)))),6,1);
abs = [as(1) 0 0 bs(1) 0 0;
as(2) as(1) 0 bs(2) bs(1) 0;
as(3) as(2) as(1) bs(3) bs(2) bs(1);
as(4) as(3) as(2) bs(4) bs(3) bs(2);
0 as(4) as(3) 0 bs(4) bs(3);
0 0 as(4) 0 0 bs(4)];
pqs = linsolve(abs, cs);
ps = reshape(pqs(1:3), 1, 3);
qs = reshape(pqs(4:6), 1, 3);
sys_c = tf(double(qs), double(ps));
sys_cl = feedback(sys, sys_c);
figure;
step(sys_cl);
disp(sys_c);
disp(pole(sys_cl));
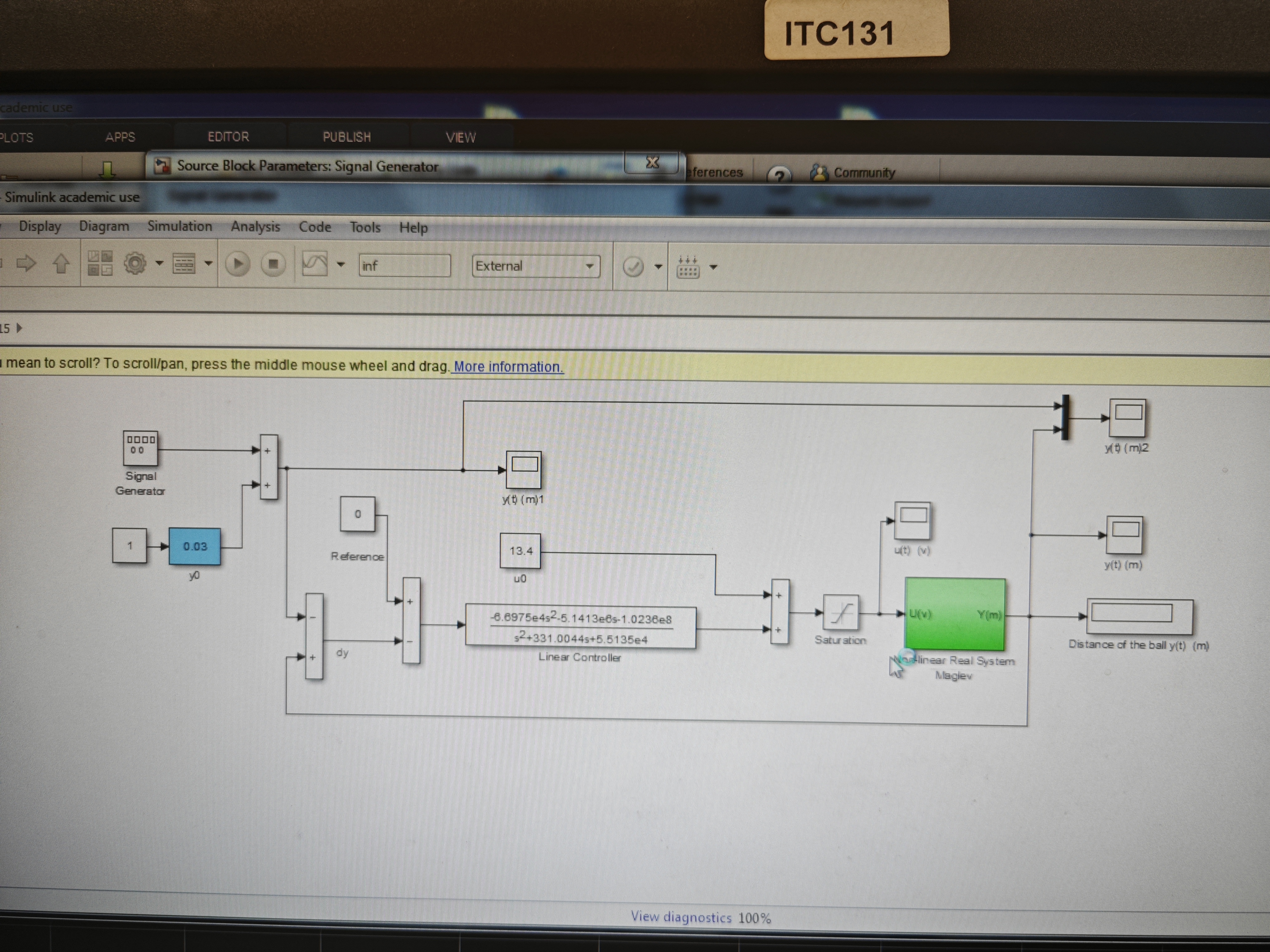
SIMULINK
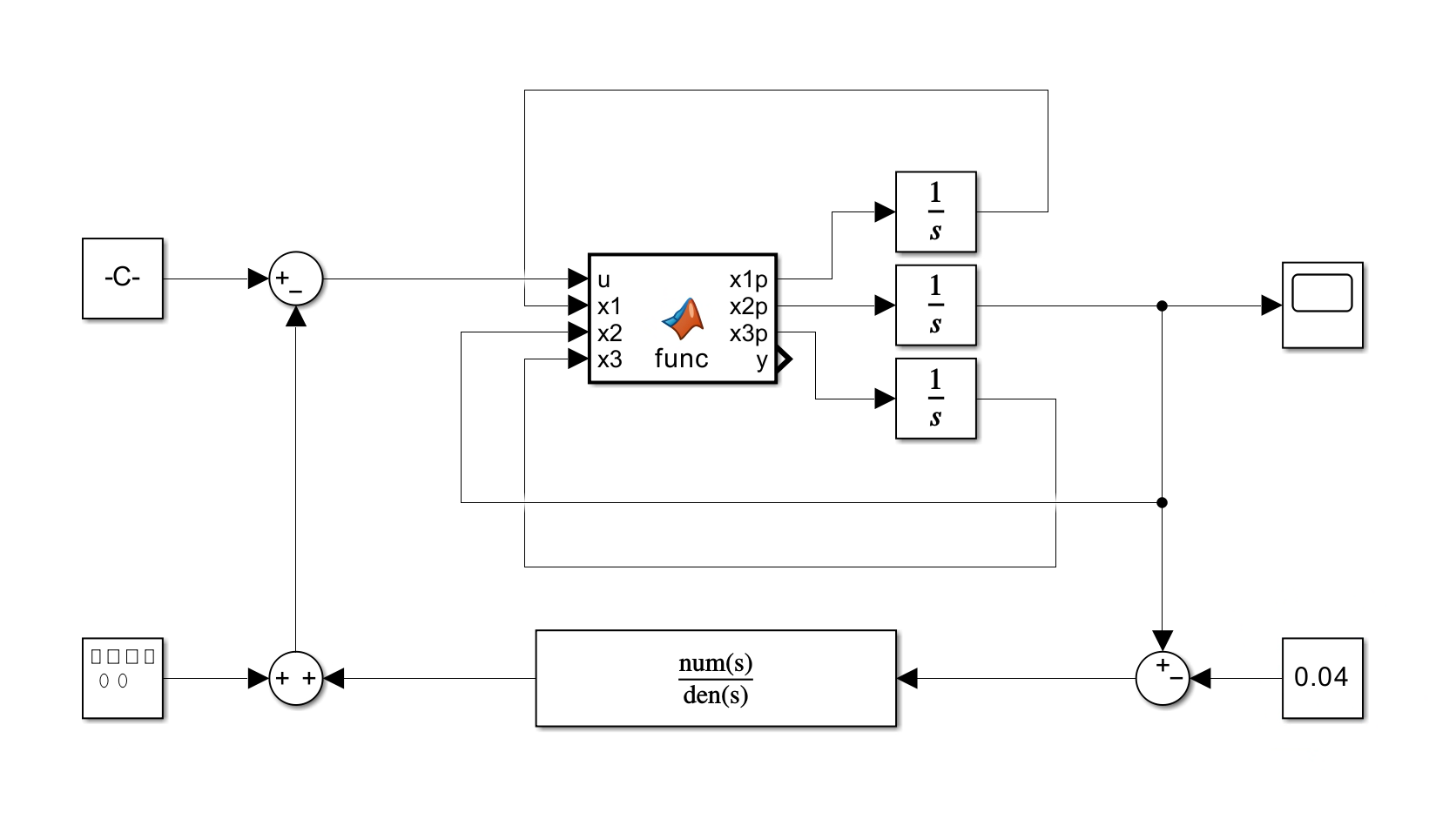
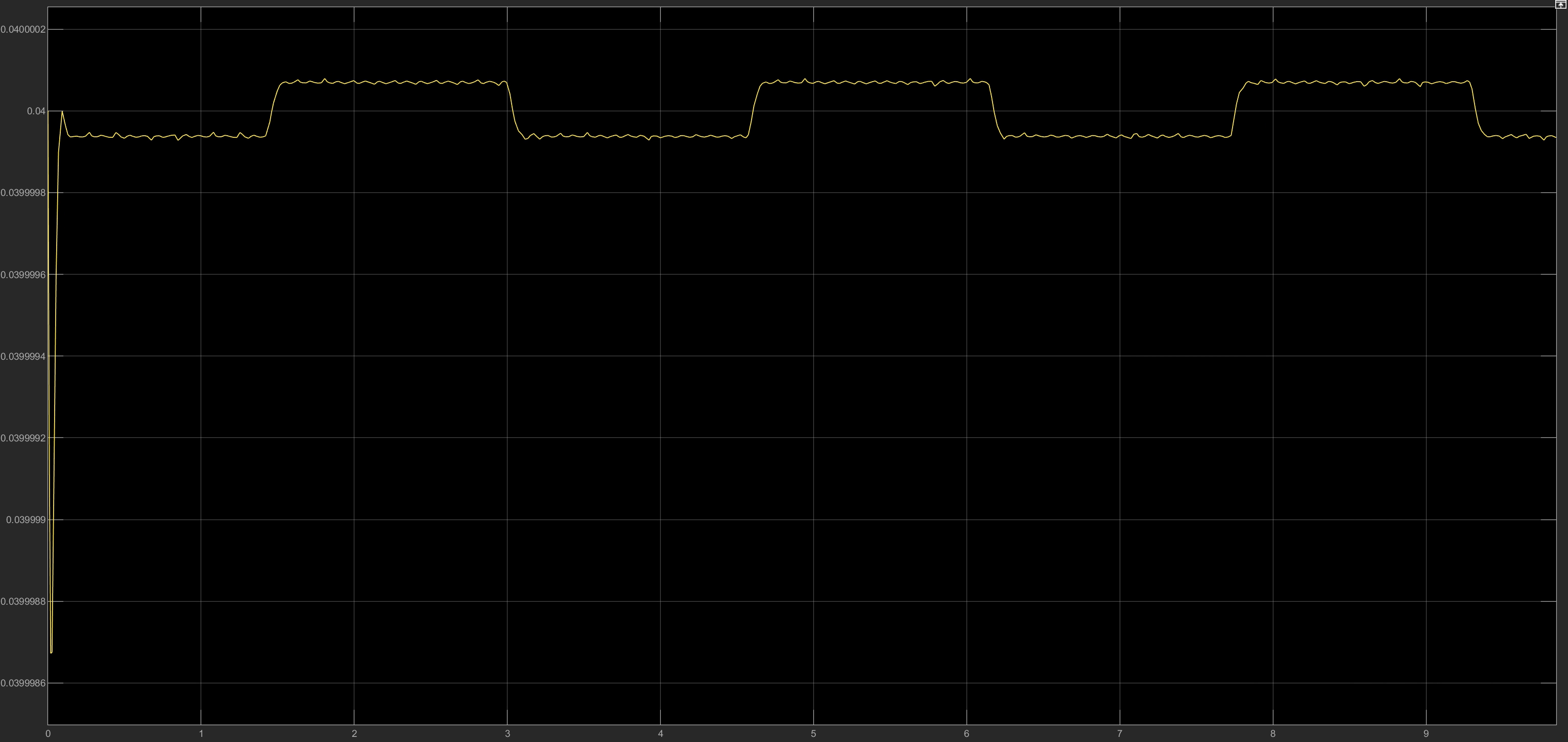
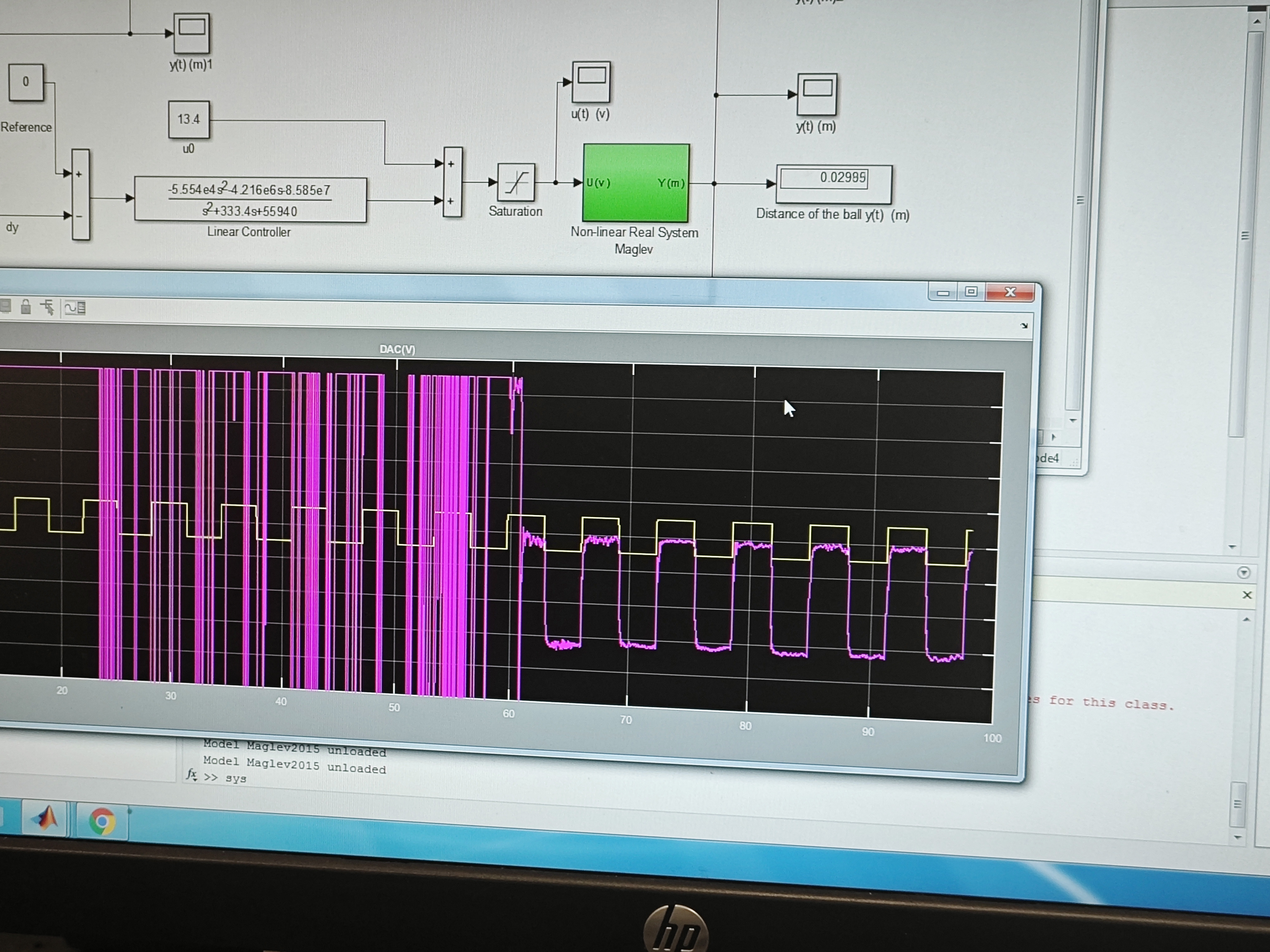
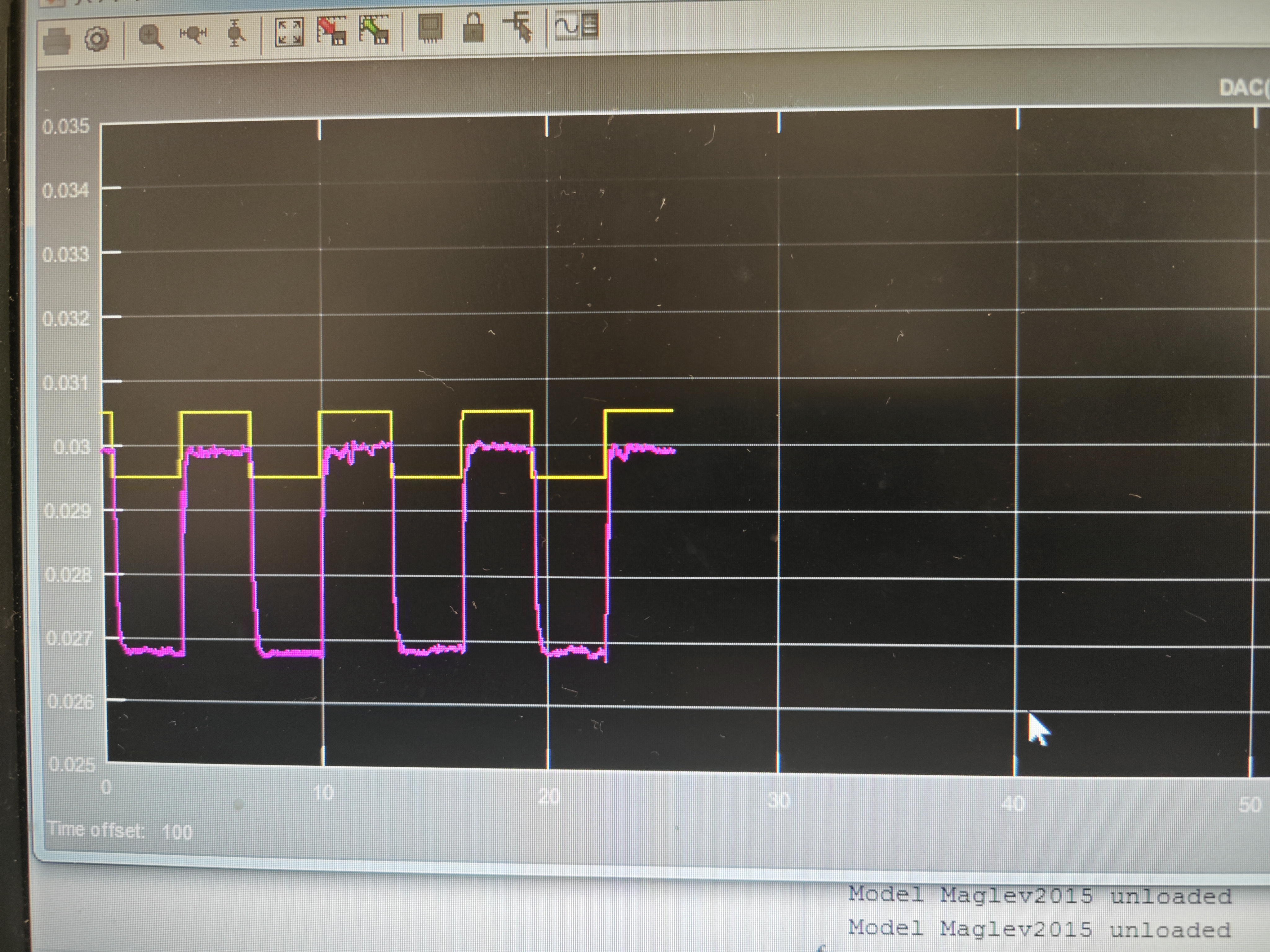
Results