A Continuous-time Representation for VINS

S. Lovegrove, A. Patron-Perez, and G. Sibley, “Spline Fusion: A continuous-time representation for visual-inertial fusion with application to rolling shutter cameras,” in Procedings of the British Machine Vision Conference 2013, Bristol: British Machine Vision Association, 2013, p. 93.1-93.11. doi: 10.5244/C.27.93.

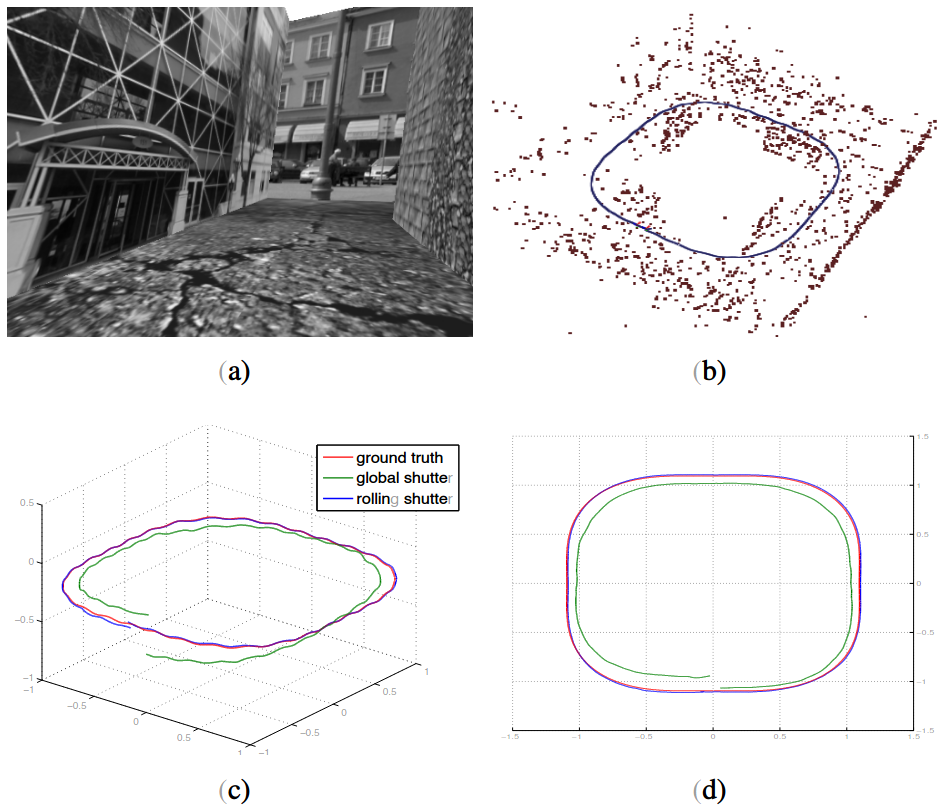
这篇论文主要工作是建立了卷帘相机的连续时域下的数学模型，初始化方法是利用 IMU 主动对齐视觉。

---

相比离散时域，在连续时域上表示有助于融合高帧率的传感器和异步时间戳的设备。对卷帘相机的研究尚未成熟，现有的工作主要集中在如何消除卷帘相机的畸变，而后复用标准全局快门相机的 SLAM 模型，这种解耦合的处理方式增加了无法修正的偏差。

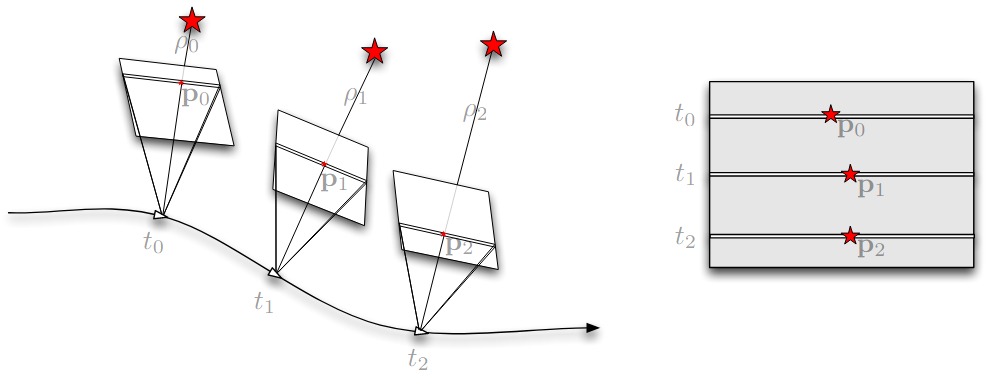
单目视觉系统存在 7 自由度不可观：6 自由度姿态+尺度，一种方法通过回环检测和序列图松弛对尺度显式参数化，另一种方法是加入可以测量绝对尺度的设备。在本文中作者使用了惯性单元。相比过往建立在欧拉角上的数学表示，作者引入李群和李代数上的旋转表示避免了奇异点，同时能够更好地近似最小扭矩的轨迹。

$${\mathbf{T}}_{b,a}=\left[\begin{array}{cc}{\mathbf{R}}_{b,a}& {\mathbf{a}}_b\\ {\mathbf{0}}^T& 1\end{array}\right],{\mathbf{T}}_{b,a}\in \mathbb{SE}3,{\mathbf{R}}_{b,a}\in \mathbb{SO}3$$

作者希望轨迹的参数化方程是局部可控，二阶导连续，能近似最小力矩轨迹的。三次 B 样条曲线可以很好表示 ${\mathbb{R}}^3$ 上的轨迹，但在三维旋转上表现一般。因此作者选用了李代数上的累计基函数，这种函数最早被应用在计算机动画中的四元数插值中。

自由度为 $k-1$ 的 B 样条曲线的标准基函数表示为

$$\begin{array}{rl}\mathbf{p}(t)& =\sum _{i=0}^n{\mathbf{p}}_i{B}_{i,k}(t)\\ & ={\mathbf{p}}_0{B}_{0,k}(t)+{\mathbf{p}}_1{B}_{1,k}(t)+\cdots +{\mathbf{p}}_n{B}_{n,k}(t)\\ & ={\mathbf{p}}_0{B}_{0,k}(t)+\sum _{i=1}^{n-1}{\mathbf{p}}_i{B}_{i,k}(t)+{\mathbf{p}}_n{B}_{n,k}(t)\\ & ={\mathbf{p}}_0{\tilde{B}}_{0,k}(t)+\sum _{i=1}^n{\mathbf{p}}_i\sum _{j=i}^n{B}_{j,k}(t)-\sum _{i=0}^{n-1}{\mathbf{p}}_i\sum _{j=i+1}^n{B}_{j,k}(t)\\ & ={\mathbf{p}}_0{\tilde{B}}_{0,k}(t)+\sum _{i=1}^n({\mathbf{p}}_i-{\mathbf{p}}_{i-1}){\tilde{B}}_{i,k}(t)\end{array}$$

其中 ${\mathbf{p}}_i\in {\mathbb{R}}^N$ 是在 $t_i,i\in [0,\dots ,n]$ 时刻的控制点，$B_{i,k}(t)$ 是由德伯尔-考克斯递归公式 De Boor - Cox recursive formula 计算得到的基函数。进一步利用李群的指数映射和对数映射，将公式重写在李群域上

$${\mathbf{T}}_{w,s}(t)=\exp ({\tilde{B}}_{0,k}\log ({\mathbf{T}}_{w,0}))\prod _{i=1}\exp ({\tilde{B}}_{i,k}(t)\log ({\mathbf{T}}_{w,i-1}^{-1}{\mathbf{T}}_{w,i}))$$

作者进一步在假设控制点时间间隔不变的情况下（大多数单目系统应该都能满足），对时间做了归一化处理

$$u(t)=\frac{t-t_0}{\mathrm{\Delta }t}-s_i$$

并在参数 $k=4$ 下转化为矩阵表达

$$\tilde{\mathbf{B}}(u)=\mathbf{C}\left[\begin{array}{c}1\\ u\\ u^2\\ u^3\end{array}\right],\dot{\tilde{\mathbf{B}}}(u)=\mathbf{C}\left[\begin{array}{c}0\\ 1\\ 2u\\ 3u^2\end{array}\right],\ddot{\tilde{\mathbf{B}}}(u)=\mathbf{C}\left[\begin{array}{c}0\\ 0\\ 2\\ 6u\end{array}\right],\mathbf{C}=\frac{1}{6}\left[\begin{array}{cccc}6& 0& 0& 0\\ 5& 3& -3& 1\\ 1& 3& 3& -2\\ 0& 0& 0& 1\end{array}\right]$$$${\mathbf{T}}_{w,s}(u)={\mathbf{T}}_{w,i-1}\prod _{j=1}^3\exp (\tilde{\mathbf{B}}(u{)}_j\log ({\mathbf{T}}_{w,i+j-1}^{-1}{\mathbf{T}}_{w,i+j}))$$

${\dot{\mathbf{T}}}_{w,s},{\ddot{\mathbf{T}}}_{w,s}$ 则由链式法则和指数映射的一阶近似得到

给定第一次观测的逆深度 $\mathbb{R}ho\in {\mathbb{R}}^{+}$, 对应点在两帧的坐标分别为 ${\mathbf{p}}_a,{\mathbf{p}}_b\in {\mathbb{R}}^2$, 其中 $\pi (\mathbf{P})=\frac{1}{P_2}[P_0,P_1{]}^T$

$${\mathbf{p}}_b=\mathcal{W}({\mathbf{p}}_a;{\mathbf{T}}_{b,a},\mathbb{R}ho)=\pi (\left[\begin{array}{cc}{\mathbf{K}}_b& \mathbf{0}\end{array}\right]{\mathbf{T}}_{b,a}\left[\begin{array}{cc}{\mathbf{K}}_a^{-1}\left[\begin{array}{c}{\mathbf{p}}_a\\ 1\end{array}\right]& \mathbb{R}ho\end{array}\right])$$

对于一般的视觉惯性系统给出损失函数

$$\begin{array}{rl}E(\theta )=& \sum _{{\hat{\mathbf{p}}}_m}{[{\hat{\mathbf{p}}}_m-\mathcal{W}({\mathbf{p}}_r;{\mathbf{T}}_{c,s}{\mathbf{T}}_{w,s}(u_m{)}^{-1}{\mathbf{T}}_{w,s}(u_r){\mathbf{T}}_{s,c},\rho )]}_{{\mathrm{\Sigma }}_p}^2+\\ & \sum _{{\hat{\omega }}_m}[{\hat{\omega }}_m-\text{Gyro}(u_m){]}_{{\mathrm{\Sigma }}_{\omega }}^2+\sum _{{\hat{\mathbf{a}}}_m}[{\hat{\mathbf{a}}}_m-\text{Accel}(u_m){]}_{{\mathrm{\Sigma }}_{\mathbf{a}}}^2\end{array}$$

而对卷帘相机则将 ${\mathbf{p}}_b$ 用 ${\mathbf{p}}_b(t)$ 替代重新建模

$${\mathbf{p}}_b(t)=\left[\begin{array}{c}{x}_b(t)\\ y_b(t)\end{array}\right]=\mathcal{W}({\mathbf{p}}_a;{\mathbf{T}}_{b,a}(t),\rho )$$$${\mathbf{p}}_b(t+\mathrm{\Delta }t)=\mathcal{W}({\mathbf{p}}_a;{\mathbf{T}}_{b,a}(t),\rho )+\mathrm{\Delta }t\cdot \frac{\partial }{\partial t}\mathcal{W}({\mathbf{p}}_a;{\mathbf{T}}_{b,a}(t),\rho )$$$$y_b(t+\mathrm{\Delta }t)=\frac{h(t+\mathrm{\Delta }t-s)}{e-s},\mathrm{\Delta }t=-\frac{h\cdot t_0+s\cdot (y_b(t)-h)-e\cdot y_b(t)}{(s-e)\frac{\partial }{\partial t}{\mathcal{W}}_y({\mathbf{p}}_a;{\mathbf{T}}_{b,a}(t),\rho )+h}$$

这一系统表现出了良好的自校准的能力