PHR Conic Augmented Lagrangian Method

Slide: Starting from the penalty method, we extend to the augmented Lagrangian method for improved stability. By introducing $s$, symmetric cone constraints are integrated, forming a unified framework for solving constrained optimization problems iteratively. Inspired by Dr. Zhepei Wang's Lecture "Numerical Optimization for Robotics".

Introduction

Penalty Method

Consider the constrained optimization problem:

$$\underset{x}{min}f(x)\text{s.t.}h(x)=0$$

Penalty method solves a series of unconstrained problems:

$$Q_{\rho }(x)=f(x)+\frac{\rho }{2}||h(x)|{|}^2$$

Challenge:

• Requires $\rho \to \mathrm{\infty }$ for exact solution, causing ill-conditioned Hessian.
• Finite $\rho$ leads to constraint violation $h(x)\ne 0$.

Lagrangian Relaxation

The Lagrangian is defined as:

$$\mathcal{L}(x,\lambda )=f(x)+{\lambda }^{\mathrm{\top }}h(x)$$

At the optimal solution $x^{\ast }$, there exists ${\lambda }^{\ast }$ such that ${\mathrm{\nabla }}_x\mathcal{L}(x^{\ast },{\lambda }^{\ast })=0$.

Uzawa's method iteratively updates $x$ and $\lambda$:

$$\{\begin{array}{l}{x}^{k+1}=\arg \underset{x}{min}\mathcal{L}(x,{\lambda }^k)\\ {\lambda }^{k+1}={\lambda }^k+{\alpha }_{k}h(x^{k+1})\end{array}$$

where ${\alpha }_k>0$ is a step size.

However, when $\lambda$ is fixed and one attempts to minimize $\mathcal{L}(x,\lambda )$:

• $\underset{x}{min}\mathcal{L}(x,\lambda )$ can be non-smooth even for smooth $f$ and $h$.
• $\underset{x}{min}\mathcal{L}(x,\lambda )$ may be unbounded or have no finite solution.

Equality Constraint

PHR Augmented Lagrangian Method

Consider the optimization problem with a penalty on the deviation from a prior $\overline{\lambda }$:

$$\underset{x}{min}\underset{\lambda }{max}f(x)+{\lambda }^{\mathrm{\top }}h(x)-\frac{1}{2\rho }||\lambda -\overline{\lambda }|{|}^2$$

The inner problem:

$${\mathrm{\nabla }}_{\lambda }=h(x)-\frac{1}{\rho }(\lambda -\overline{\lambda })\Rightarrow {\lambda }^{\ast }(\overline{\lambda })=\overline{\lambda }+\rho h(x)$$

The outer problem:

$$\begin{array}{rl}& \underset{x}{min}\underset{\lambda }{max}f(x)+{\lambda }^{\mathrm{\top }}h(x)-\frac{1}{2\rho }||\lambda -\overline{\lambda }|{|}^2\\ =& \underset{x}{min}f(x)+[{\lambda }^{\ast }(\overline{\lambda }){]}^{\mathrm{\top }}h(x)-\frac{1}{2\rho }||{\lambda }^{\ast }(\overline{\lambda })-\overline{\lambda }|{|}^2\\ =& \underset{x}{min}f(x)+[\overline{\lambda }+\rho h(x){]}^{\mathrm{\top }}h(x)-\frac{\rho }{2}||h(x)|{|}^2\\ =& \underset{x}{min}f(x)+{\overline{\lambda }}^{\mathrm{\top }}h(x)+\frac{\rho }{2}||h(x)|{|}^2\end{array}$$

PHR Augmented Lagrangian Method (cont.)

To increase precision:

• Reduce the penalty weight $1/\rho$
• Update the prior multiplier $\overline{\lambda }\leftarrow {\lambda }^{\ast }(\overline{\lambda })$

Uzawa's method for the augmented Lagrangian function is:

1. $x\leftarrow \arg \underset{x}{min}f(x)+{\overline{\lambda }}^{\mathrm{\top }}h(x)+\frac{\rho }{2}||h(x)|{|}^2$
2. $\overline{\lambda }\leftarrow \overline{\lambda }+\rho h(x)$

Penalty Method Perspective

The corresponding primal problem of the augumented Lagrangian Function is obviously:

$$\begin{array}{rl}\underset{x}{min}& f(x)+\frac{\rho }{2}||h(x)|{|}^2\\ \text{s.t. }& h(x)=0\end{array}$$

Advantages:

• Even without $\rho \to \mathrm{\infty }$, the constraints can be exactly satisfied in the limit through multiplier updates.
• For large $\rho$, the penalty term $\frac{\rho }{2}||h(x)|{|}^2$ dominates, ensuring $\underset{x}{min}{\mathcal{L}}_{\rho }(x,\lambda )$ has a local solution.
• The augmented dual function $q_{\rho }(\lambda )$ is smooth in proper conditions, with $\mathrm{\nabla }{q}_{\rho }(\lambda )\approx h(x(\lambda ))$.

Practical PHR-ALM

In practical, we use its equivalent form:

$${\mathcal{L}}_{\rho }(x,\lambda )=f(x)+\frac{\rho }{2}{\Vert h(x)+\frac{\lambda }{\rho }\Vert }^2-\underset{x\text{-independent}}{\underbrace{\frac{1}{2\rho }||\lambda |{|}^2}}$$

The KKT solution can be solved via:

$$\{\begin{array}{l}{x}^{k+1}=\arg \underset{x}{min}{\mathcal{L}}_{{\rho }^k}(x,{\lambda }^k)\\ {\lambda }^{k+1}={\lambda }^k+{\rho }^{k}h(x^{k+1})\\ {\rho }^{k+1}=min[(1+\gamma ){\rho }^k,{\rho }_{max}]\end{array}$$

where ${\rho }^k$ can be any nondecreasing positive sequence.

Inequality Constraint

Slack Variables Relaxation

Consider the optimization problem with inequality constraints:

$$\underset{x}{min}f(x)\text{s.t.}g(x)\le 0$$

We use the equivalent formulation using slack variables:

$$\underset{x,s}{min}f(x)\text{s.t.}g(x)+[s{]}^2=0$$

where $[\cdot {]}^2$ means element-wise squaring.

We can directly form Lagrangian like equality-constrained case

$$\begin{array}{rl}& \underset{x,s}{min}\{f(x)+\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2\}\\ =& \underset{x}{min}f(x)+\underset{x}{min}\underset{s}{min}\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2\\ =& \underset{x}{min}f(x)+\frac{\rho }{2}{\Vert max[g(x)+\frac{\lambda }{\rho },0]\Vert }^2\end{array}$$

Simplified Form

Summing over all components gives the final form:

$${\mathcal{L}}_{\rho }(x,\mu )=f(x)+\frac{\rho }{2}{\Vert max[g(x)+\frac{\mu }{\rho },0]\Vert }^2-\underset{x\text{-independent}}{\underbrace{\frac{1}{2\rho }||\mu |{|}^2}}$$

For the dual update, from the optimality condition:

$$\begin{array}{rl}{\mu }^{k+1}& ={\mu }^k+\rho (g(x^{k+1})+[s^{k+1}{]}^2)\\ & =max[{\mu }^k+\rho g(x^{k+1}),0]\end{array}$$

Summary

PHR Augmented Lagrangian Method for General Nonconvex cases:

$$\begin{array}{rl}\underset{x}{min}& f(x)\\ \text{s.t. }& h(x)=0\\ & g(x)\le 0\end{array}$$

Its PHR Augmented Lagrangian is defined as

$${\mathcal{L}}_{\rho }=f(x)+\frac{\rho }{2}{\Vert h(x)+\frac{\lambda }{\rho }\Vert }^2+\frac{\rho }{2}{\Vert max[g(x)+\frac{\mu }{\rho },0]\Vert }^2-\frac{1}{2\rho }\{||\lambda |{|}^2+||\mu |{|}^2\}$$

The PHR-ALM is simply repeating the primal descent and dual ascent iterations:

$$\{\begin{array}{l}{x}^{k+1}=\arg \underset{x}{min}{\mathcal{L}}_{{\rho }^k}(x,{\lambda }^k,{\mu }^k)\\ {\lambda }^{k+1}={\lambda }^k+{\rho }^{k}h(x^{k+1})\\ {\mu }^{k+1}=max[{\mu }^k+{\rho }^{k}g(x^{k+1}),0]\\ {\rho }^{k+1}=min[(1+\gamma ){\rho }^k,{\rho }_{max}]\end{array}$$

Courtesy: Z. Wang

Symmetric Cone Constraint

Extension to Symmetric Cone Constraints

Consider the symmetric cone constrained optimization problem:

$$\begin{array}{rl}\underset{x}{min}& f(x)\\ \text{s.t. }& h(x)=0\\ & g(x)\in \mathcal{K}\end{array}$$

Second Order Cone	Positive Definite Cone

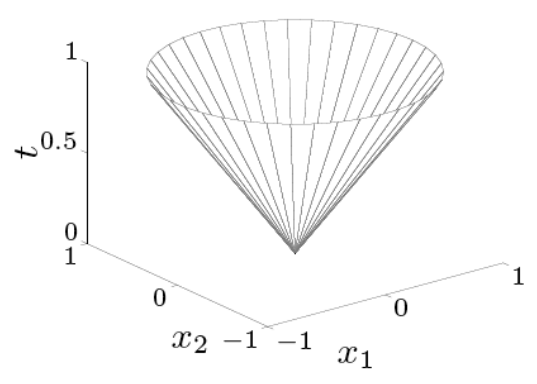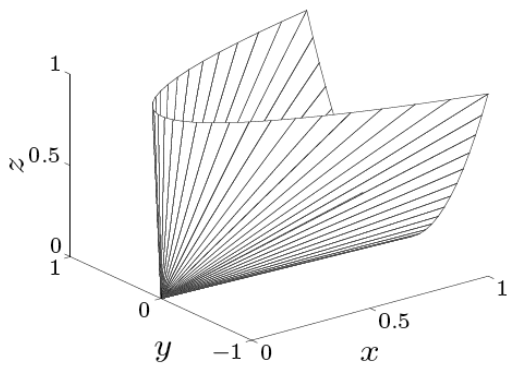Generalized Inequality Constraint

For the symmetric cone constraint $x\in \mathcal{K}$, we can equivalently express it as:

$$g(x)=-x{⪯}_{\mathcal{K}}0$$

The standard inequality constraint $g(x)\le 0$ corresponds to the nonnegative orthant cone:

$$\mathcal{K}={\mathbb{R}}_{+}^n=\{x\in {\mathbb{R}}^n:x_i\ge 0,i=1,\dots ,n\}$$

t's projection operator is exactly element-wise max function:

$${\mathrm{\Pi }}_{{\mathbb{R}}_{+}^n}(v)=max[v,0],({\mathbb{R}}_{+}^n{)}^{\ast }={\mathbb{R}}_{+}^n$$

Slack Variables Relaxation

Consider the optimization problem with inequality constraints:

$$\underset{x}{min}f(x)\text{s.t.}g(x)\in \mathcal{K}$$

By Euclidean Jordan algebra, the conit program is equivalent to

$$\underset{x,s}{min}f(x)\text{s.t.}g(x)=s\circ s$$

We can directly form Lagrangian like equality-constrained case

$$\begin{array}{rl}& \underset{x,s}{min}\{f(x)+\frac{\rho }{2}{\Vert g(x)-s\circ s+\frac{\lambda }{\rho }\Vert }^2\}\\ =& \underset{x}{min}f(x)+\underset{x}{min}\underset{s}{min}\frac{\rho }{2}{\Vert g(x)-s\circ s+\frac{\lambda }{\rho }\Vert }^2\\ =& \underset{x}{min}f(x)+\frac{\rho }{2}{\Vert {\mathrm{\Pi }}_{\mathcal{K}}(-g(x)-\frac{\lambda }{\rho })\Vert }^2\end{array}$$

Simplified Form

Let $\mu =-\lambda$, we get the final form:

$${\mathcal{L}}_{\rho }(x,\mu )=f(x)+\frac{\rho }{2}{\Vert {\mathrm{\Pi }}_{{\mathcal{K}}^{\mathcal{\ast }}}(-g(x)+\frac{\mu }{\rho })\Vert }^2-\underset{x\text{-independent}}{\underbrace{\frac{1}{2\rho }||\mu |{|}^2}}$$

For the dual update, from the optimality condition:

$$\begin{array}{rl}{\mu }^{k+1}& ={\mu }^k+\rho [g(x^{k+1})-s^{k+1}\circ s^{k+1}]\\ & ={\mathrm{\Pi }}_{{\mathcal{K}}^{\mathcal{\ast }}}[{\mu }^k-\rho \cdot g(x^{k+1})]\end{array}$$

where ${\mathcal{K}}^{\ast }$ is the dual cone of $\mathcal{K}$.

Summary

PHR Augmented Lagrangian Method for General Nonconvex cases:

$$\begin{array}{rl}\underset{x}{min}& f(x)\\ \text{s.t. }& h(x)=0\\ & g(x)\in \mathcal{K}\end{array}$$

Its PHR Augmented Lagrangian is defined as

$${\mathcal{L}}_{\rho }=f(x)+\frac{\rho }{2}{\Vert h(x)+\frac{\lambda }{\rho }\Vert }^2+\frac{\rho }{2}{\Vert {\mathrm{\Pi }}_{\mathcal{K}}(-g(x)+\frac{\mu }{\rho })\Vert }^2-\frac{1}{2\rho }\{||\lambda |{|}^2+||\mu |{|}^2\}$$

The PHR-ALM is simply repeating the primal descent and dual ascent iterations:

$$\{\begin{array}{l}{x}^{k+1}=\arg \underset{x}{min}{\mathcal{L}}_{{\rho }^k}(x,{\lambda }^k,{\mu }^k)\\ {\lambda }^{k+1}={\lambda }^k+{\rho }^{k}h(x^{k+1})\\ {\mu }^{k+1}={\mathrm{\Pi }}_{{\mathcal{K}}^{\mathcal{\ast }}}({\mu }^k-{\rho }^k{x}^{k+1})\\ {\rho }^{k+1}=min[(1+\gamma ){\rho }^k,{\rho }_{max}]\end{array}$$