KKT Conditions and Optimization Techniques

Slide: This lecture begins with an introduction to the Karush-Kuhn-Tucker (KKT) conditions, which are fundamental in constrained optimization. We will explore their geometric interpretation, derive the necessary conditions for optimality, and discuss their applications in solving optimization problems.

Lagrangian Multiplier

Optimization with Equality Constraints

Consider an optimization problem with equality constraints:

$$\begin{array}{r}\underset{x}{min}f(x)\text{subject to}{h}_j(x)=0\end{array}$$

how to characterize the necessary conditions for the optimal solution $x^{\ast }$ ?

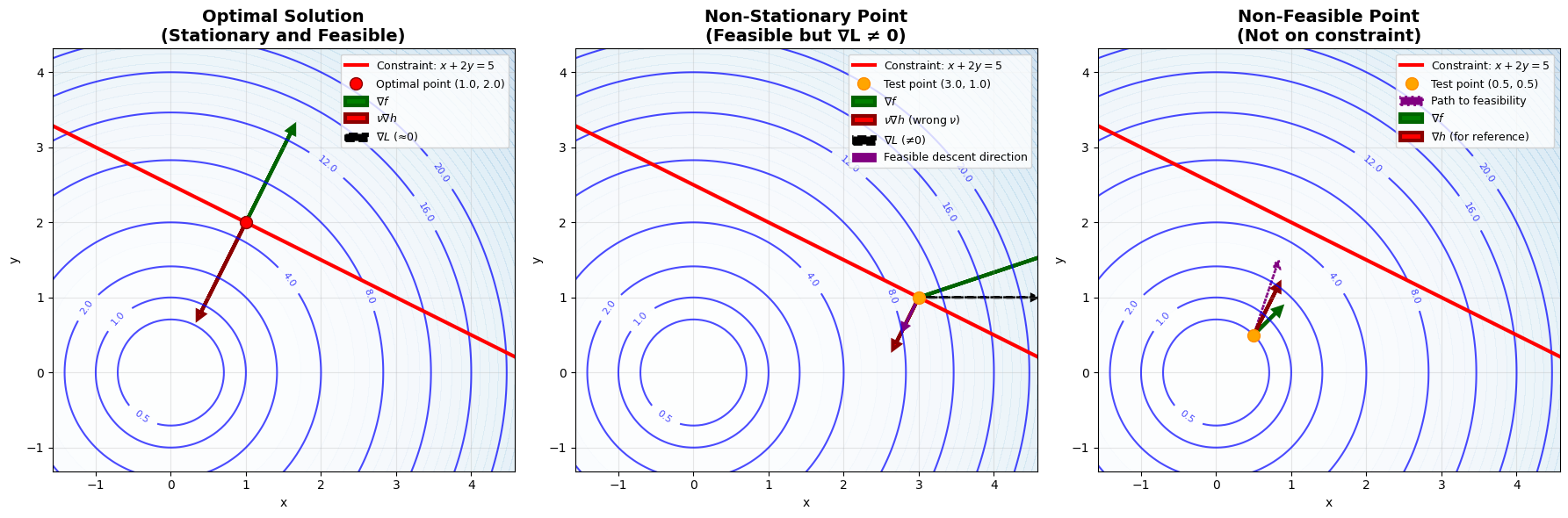
Geometric Insight

Consider a quadratic objective function with one linear equality constraint:

$$\underset{x,y}{min}{x}^2+y^2\text{subject to}x+2y=5$$

$\mathrm{\nabla }f(x^{\ast })$ must lie within the linear subspace spanned by $\{\mathrm{\nabla }{h}_j(x^{\ast })\}$; otherwise, the function value could be further decreased by moving along a feasible direction. This means there exist multipliers $\{{\nu }_j^{\ast }\}$ such that:

$$\mathrm{\nabla }f(x^{\ast })+\sum _j{\nu }_j^{\ast }\mathrm{\nabla }{h}_j(x^{\ast })=0$$

Lagrangian Function and Optimality Conditions

We introduce the Lagrangian function as a tool to characterize optimality:

$$\mathcal{L}(x,\nu )=f(x)+\sum _j{\nu }_j{h}_j(x)$$

The necessary conditions for optimality can be expressed as stationarity of the Lagrangian:

$$\mathrm{\nabla }\mathcal{L}(x^{\ast },{\nu }^{\ast })=0⟺\{\begin{array}{l}{\mathrm{\nabla }}_x\mathcal{L}=\mathrm{\nabla }f(x^{\ast })+\sum _j{\nu }_j^{\ast }\mathrm{\nabla }{h}_j(x^{\ast })=0\\ {\mathrm{\nabla }}_{\nu }\mathcal{L}=[\dots ,h_j(x^{\ast }),\dots {]}^{\mathrm{\top }}=0\end{array}$$

Lagrangian Relaxation

A Min-Max Interpretation

The Lagrangian function also leads to a powerful dual interpretation:

$$\underset{\nu }{max}\mathcal{L}(x,\nu )=\{\begin{array}{ll}f(x),& h_j(x)=0\\ \mathrm{\infty },& \text{otherwise}\end{array}$$

The original constrained problem is equivalent to the following min-max problem:

$$\underset{x}{min}f(x),\text{s.t.}{h}_j(x)=0⟺\underset{x}{min}\underset{\nu }{max}\mathcal{L}(x,\nu )$$

The Dual Problem and Weak Duality

Solution for $\underset{x}{min}\underset{\nu }{max}\mathcal{L}(x,\nu )$ may be non-continuous, but solution for $\underset{\nu }{max}\underset{x}{min}\mathcal{L}(x,\nu )$ is easy if $\mathcal{L}(x,\nu )$ is tractable. We can form the dual problem by swapping the order of the min and the max:

$$\underset{\nu }{max}d(\nu )=\underset{\nu }{max}\underset{x}{min}\mathcal{L}(x,\nu )\le \underset{x}{min}\underset{\nu }{max}\mathcal{L}(x,\nu )$$

Under some conditions, equality holds, which means strong duality holds.

Uzawa's Method (Dual Ascent)

$$\mathrm{\nabla }d(\nu )=h[x^{\ast }(\nu )]\text{where}{x}^{\ast }(\nu )=\arg \underset{x}{min}\mathcal{L}(x,\nu )$$

This leads to Uzawa's Method:

1. Minimization ($x$-step):$$x^{k+1}=\arg \underset{x}{min}\mathcal{L}(x,{\nu }^k)$$
2. Ascent ($\nu$-step):$${\nu }^{k+1}={\nu }^k+{\alpha }^{k}h(x^{k+1})$$where ${\alpha }^k>0$ is the step size.

KKT Conditions

General Constrained Optimization

Consider a general optimization problem with equality and inequality constraints:

$$\begin{array}{rl}\underset{x}{min}& f(x)\\ \text{s.t. }& g_i(x)\le 0\\ & h_j(x)=0\end{array}$$

the question does not change: how to characterize the necessary conditions for the optimal solution $x^{\ast }$ ?

Geometric Insight

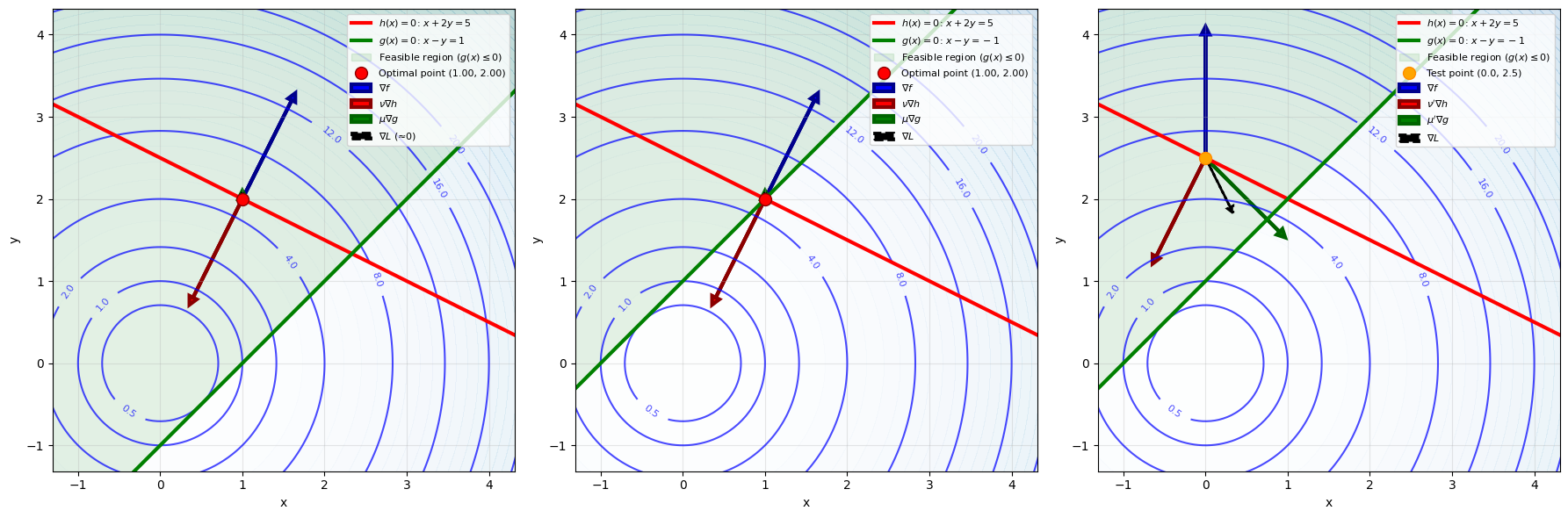
Challenge:

1. Directionality: On the boundary, $\mathrm{\nabla }{g}_i$ points towards the exterior of the feasible region. To prevent $f$ from pushing the point into an infeasible area, $\mathrm{\nabla }f$ must have a component opposite to $\mathrm{\nabla }{g}_i$ $⟹$ ${\mu }_i\ge 0$.
2. Activity Identification: The optimum may lie in the interior of the region with $g_i<0$ or on the boundary with $g_i=0$ $⟹$ ${\mu }_i{g}_i=0$.

Summary

1. Stationarity: $0\in {\partial }_x[f(x)+\sum _i{\mu }_i{g}_i(x)+\sum _j{\nu }_j{h}_j(x)]$
2. Complementary Slackness: ${\mu }_i{g}_i(x)=0$
3. Primal Feasibility: $g_i(x)\le 0,h_j(x)=0$
4. Dual Feasibility: ${\mu }_i\ge 0$