Report for Cyber Planner Code Report

We have already launched our report for Cyber Planner from Next Innovation STEM Center. You can also find a copy here. And the source code is available in our Github repository.

While Cyber Planner Code Report v0.1.0 (C++ Version) is mainly focused on the Math derivation, Report for Cyber Planner Code Report emphasize the corresponding code of the equation and highlight some details in the implementation. I believe it would bring you a different perspective to our work and enhance your understaning in numerical optimization.

Convex Polytope Set

Any object can be represented by a finite convex polytope set. And a convex polytope can be represented by a group of linear inequalities. If a point is inside the polytope, it should satisfied:

$$Ax⪯b$$

Distance from Point to Polytope

If the point is inside the polytope, the distance is the negative minimum distance to any support hyperplane of the polytope. Which is given by:

$$-min\{\frac{A_{i}p-b_i}{||A_i||}\}$$

Otherwise, we are going to find a point inside the polytope, which has the minimum distance to the original point.

$$\underset{x\in \mathcal{S}}{min}||x-p|{|}^2$$

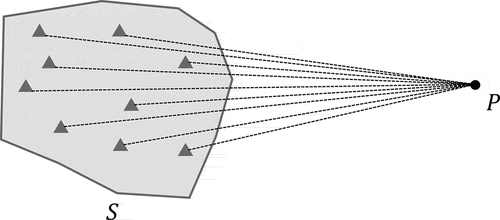
It refers to the Eq. 6 in report and can be solved by LDQP (Low Dimensional Quadratic Programming) easily.

Click me to toggle the code

Polygon.hpp

class Polygon {
 private:
    // Ax <= b
    Eigen::MatrixX2d A;
    Eigen::VectorXd b;

 public:
  bool isPointInside(Eigen::Vector2d p) {
    return (this->A * p - this->b).maxCoeff() <= 0;
  }

  double distanceToPoint(Eigen::Vector2d p) {
    if (this->isPointInside(p)) {
        double result = INFINITY;
        for (int i = 0; i < this->points.size(); i++) {
        result = std::min(result,
                            (b(i) - A.row(i).dot(p)) / (A.row(i).norm() + 1e-20));
        }
        return -result;
    }
    if (A.rows() == 1) {
        return (A.row(0).dot(p) - b(0)) / (A.row(0).norm() + 1e-20);
    }
    Eigen::Vector2d x = p;
    sdqp::sdqp<2>(2 * Eigen::MatrixXd::Identity(2, 2), -2 * p, A, b, x);
    return (p - x).norm();
  }
};

Distance from Polytope to Polytope

The distance between two polytopes is the minimum distance between any two points in the two polytopes. If the two polytopes are intersected, it is easy. The distance is defined as the minimum distance from a point contained in another polytope to that polytope.

If the two polytopes are not intersected, the distance is the minimum distance between any point in the first polytope and any point in the second polytope.

$$\underset{x\in {\mathcal{S}}_1,y\in {\mathcal{S}}_2}{min}||x-y|{|}^2$$

$x$ and $y$ are combined as a vector $\left[\begin{array}{c}x\\ y\end{array}\right]$. And the distance can be represented as:

$$\begin{array}{rl}& ||x-y|{|}^2\\ =& {\left|\left|\left[\begin{array}{cc}I& -I\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\right|\right|}^2\\ =& {\left|\left|\left[\begin{array}{cc}x& y\end{array}\right]\left[\begin{array}{cc}I& -I\\ -I& I\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\right|\right|}^2\end{array}$$

A LDQP is defined as $\underset{x\in \mathcal{S}}{min}\frac{1}{2}{x}^{T}Qx+c^{T}x$, while $Q$ is a positive definite matrix. In this case, $Q$ is a positive semi-definite matrix, but enough here.

Click me to toggle the code

Polygon.hpp

class Polygon {
 private:
  // Ax <= b
  Eigen::MatrixX2d A;
  Eigen::VectorXd b;

 public:
  bool isPolygonIntersect(Polygon poly) {
    // check if the two polygons intersect
    for (int i = 0; i < this->points.size(); i++) {
      Eigen::Vector2d p1 = this->points[i];
      Eigen::Vector2d p2 = this->points[(i + 1) % this->points.size()];
      for (int j = 0; j < poly.points.size(); j++) {
        Eigen::Vector2d q1 = poly.points[j];
        Eigen::Vector2d q2 = poly.points[(j + 1) % poly.points.size()];
        double d = (p1.x() - p2.x()) * (q1.y() - q2.y()) -
                   (p1.y() - p2.y()) * (q1.x() - q2.x());
        if (d == 0) {
          continue;
        }
        double t = ((p1.x() - q1.x()) * (q1.y() - q2.y()) -
                    (p1.y() - q1.y()) * (q1.x() - q2.x())) /
                   d;
        double u = -((p1.x() - p2.x()) * (p1.y() - q1.y()) -
                     (p1.y() - p2.y()) * (p1.x() - q1.x())) /
                   d;
        if (t >= 0 && t <= 1 && u >= 0 && u <= 1) {
          return true;
        }
      }
    }

    // check if one polygon contains another
    bool inside = true;
    for (Eigen::Vector2d p : this->points) {
      if (!poly.isPointInside(p)) {
        inside = false;
        break;
      }
    }
    if (inside) {
      return true;
    }
    for (Eigen::Vector2d p : poly.points) {
      if (!this->isPointInside(p)) {
        return false;
      }
    }
    return true;
  }

  double distanceToPolygon(Polygon poly) {
    Eigen::Vector4d x = Eigen::Vector4d::Zero();
    int n1 = this->points.size();
    int n2 = poly.points.size();
    if (this->isPolygonIntersect(poly)) {
      double result = 0;
      for (int i = 0; i < n1; i++) {
        if (poly.isPointInside(this->points[i])) {
          result = std::min(result, poly.distanceToPoint(this->points[i]));
        }
      }
      for (int i = 0; i < n2; i++) {
        if (this->isPointInside(poly.points[i])) {
          result = std::min(result, this->distanceToPoint(poly.points[i]));
        }
      }
      return result == 0 ? -INFINITY : result;
    }
    Eigen::Matrix4d Q;
    Eigen::Vector4d c;
    Q << 2, 0, -2, 0, 0, 2, 0, -2, -2, 0, 2, 0, 0, -2, 0, 2;
    c << 0, 0, 0, 0;
    Eigen::MatrixX4d c_A = Eigen::MatrixX4d::Zero(n1 + n2, 4);
    Eigen::VectorXd c_b = Eigen::VectorXd::Zero(n1 + n2);
    for (int i = 0; i < n1; i++) {
      c_A(i, 0) = this->A(i, 0);
      c_A(i, 1) = this->A(i, 1);
      c_b(i) = this->b(i);
    }
    for (int i = 0; i < n2; i++) {
      c_A(i + n1, 2) = poly.A(i, 0);
      c_A(i + n1, 3) = poly.A(i, 1);
      c_b(i + n1) = poly.b(i);
    }
    sdqp::sdqp<4>(Q, c, c_A, c_b, x);
    return (x.head(2) - x.tail(2)).norm();
  }
};

Artificial Potential Field

Potential in Grid

To avoid A Star Algorithm finding a path close to the obstacles, we can add a potential field to the grid. The potential field is defined by a 2 pass DP (dynamic programming). The first pass is to calculate the distance from the current point to the nearest obstacle whose index is less than the current point. The second pass is to calculate the distance from the current point to the nearest obstacle by mixing the first pass and the distance from the current point to the nearest obstacle whose index is greater than the current point.

Click me to toggle the code

space.hpp

void getGridMap(ObjectType type, std::vector<std::vector<double>>& map) {
  assert(type != ObjectType::ENV);
  Object env = Object(ObjectType::ENV);
  Object arm = Object(type);

  const double obstacle = OBSTACLE_OFFSET;
  const double reduce = OBSTACLE_FIELD_REDUCTION;
  map = std::vector<std::vector<double>>(
      ELEVATOR_GRID_NUMS, std::vector<double>(ARM_GRID_NUMS, true));

  // bound of the map
  for (int tt = 0; tt < ELEVATOR_GRID_NUMS; ++tt) {
    map[tt][0] = obstacle * reduce;
    map[tt][ARM_GRID_NUMS - 1] = obstacle * reduce;
  }
  for (int rr = 0; rr < ARM_GRID_NUMS; ++rr) {
    map[0][rr] = obstacle * reduce;
    map[ELEVATOR_GRID_NUMS - 1][rr] = obstacle * reduce;
  }

  // first pass
  for (int tt = 1; tt < ELEVATOR_GRID_NUMS - 1; ++tt) {
    for (int rr = 1; rr < ARM_GRID_NUMS - 1; ++rr) {
      Eigen::Vector2d tr = getTR(tt, rr);
      if (env.intersect(arm.armTransform(tr.x(), tr.y()))) {
        map[tt][rr] = obstacle;
      } else {
        double max_val = map[tt - 1][rr - 1];
        if (map[tt - 1][rr] > max_val) max_val = map[tt - 1][rr];
        if (map[tt][rr - 1] > max_val) max_val = map[tt][rr - 1];
        if (map[tt - 1][rr - 1] > max_val) max_val = map[tt - 1][rr - 1];
        map[tt][rr] = max_val * reduce;
      }
    }
  }

  // second pass
  for (int tt = ELEVATOR_GRID_NUMS - 2; tt > 0; --tt) {
    for (int rr = ARM_GRID_NUMS - 2; rr > 0; --rr) {
      if (map[tt][rr] == obstacle) continue;
      double max_val = map[tt + 1][rr + 1];
      if (map[tt + 1][rr] > max_val) max_val = map[tt + 1][rr];
      if (map[tt][rr + 1] > max_val) max_val = map[tt][rr + 1];
      if (map[tt + 1][rr + 1] > max_val) max_val = map[tt + 1][rr + 1];
      map[tt][rr] =
          map[tt][rr] > max_val * reduce ? map[tt][rr] : max_val * reduce;
    }
  }

  // ignore the value less than 1
  // for (int tt = 0; tt < ELEVATOR_GRID_NUMS; ++tt) {
  //   for (int rr = 0; rr < ARM_GRID_NUMS; ++rr) {
  //     if (map[tt][rr] < 1) {
  //       map[tt][rr] = 0;
  //     }
  //   }
  // }
  return;
}

Lipschitz Continuous

After gaining a heuristic path, we are going to smooth it and minimize it's stretch energy. The stretch energy can be integrated by the second derivative of the cubic spline interpolated path. However, although the term of the stretch energy and the exponential of the negative distance between two polygons can form a Lipschitz continuous function, but the gradient of the function cannot be solved in analytical form. The numerical form consume too much time and is not practical.

So we use another approximation method to smooth the path, which is presented in the Eq. 8 in the report. $||x_i-{\overline{x}}_i|{|}_{\mathrm{\Sigma }}^2$ is the prior term obtained by A* search. The Mahalanobis distance is used because the units of the dimensions in configuration space are different and the L2 norm is meaningless. Squaring ensures differential flatness.

$$\underset{x}{min}\left[\begin{array}{rl}& \sum _{i=0}^n||x_i-{\overline{x}}_i|{|}_{\mathrm{\Sigma }}^2+\\ & \sum _{i=1}^{n-1}||x_{i+1}-x_i|{|}_{\mathrm{\Sigma }}^2+\\ & \sum _{i=1}^{n-2}||x_{i+2}-2x_{i+1}+x_i|{|}_{\mathrm{\Sigma }}^2\end{array}\right]$$

Click me to toggle the code

Smooth.hpp

class Smooth {
 private:
  int n;
  Eigen::VectorXd x, x0;  // [t0, t1, ..., tn, r0, r1, ..., rn]'
  std::vector<Eigen::Vector2d> path;

 private:
  static double loss(void* instance, const Eigen::VectorXd& optX,
                     Eigen::VectorXd& optG) {
    Smooth* smooth = static_cast<Smooth*>(instance);
    double res = 0;
    optG = Eigen::VectorXd::Zero(optX.size());

    // length potential field
    for (int i = 0; i < smooth->n - 1; ++i) {
      double d = pow(optX(i) - optX(i + 1), 2);
      optG(i) += 2 * d;
      optG(i + 1) += -2 * d;
      res += d;

      d = pow(optX(i + smooth->n) - optX(i + smooth->n + 1), 2);
      optG(i + smooth->n) += 2 * d;
      optG(i + smooth->n + 1) += -2 * d;
      res += d;
    }

    // smoothness potential field
    for (int i = 1; i < smooth->n - 1; ++i) {
      double d = pow(optX(i - 1) - 2 * optX(i) + optX(i + 1), 2);
      optG(i - 1) += 2 * d;
      optG(i) += -4 * d;
      optG(i + 1) += 2 * d;
      res += d;

      d = pow(optX(i + smooth->n - 1) - 2 * optX(i + smooth->n) + optX(i + smooth->n + 1), 2);
      optG(i + smooth->n - 1) += 2 * d;
      optG(i + smooth->n) += -4 * d;
      optG(i + smooth->n + 1) += 2 * d;
      res += d;
    }

    // penalty term
    for (int i = 1; i < smooth->n - 1; ++i) {
      res += .5 * pow(optX(i) - smooth->x0(i), 2);
      res += .5 * pow(optX(i + smooth->n) - smooth->x0(i + smooth->n), 2);
      optG(i) += (optX(i) - smooth->x0(i));
      optG(i + smooth->n) += (optX(i + smooth->n) - smooth->x0(i + smooth->n));
    }

    optG(0) = 0;
    optG(smooth->n - 1) = 0;
    optG(smooth->n) = 0;
    optG(2 * smooth->n - 1) = 0;

    return res;
  }
};

Augumented Lagrangian Method

Iteration

Eq. 30 and Eq. 31 in the report are the objective function and the gradient of it. The corresponding code is shown below.

$$\begin{array}{rl}{\mathcal{L}}_{\rho }(x,\mu ,\nu ,\lambda ,\eta )=& c^{T}x+\\ & \frac{\rho }{2}\sum _{i=1}^m||P_{{\mathcal{K}}_i}(\frac{{\mu }_i}{\rho }-A_{i}x-b_i)|{|}^2+\\ & \frac{\rho }{2}\sum _{j=1}^q||x^T{J}_{j}x-r_j^{T}x+\frac{{\nu }_j}{\rho }|{|}^2+\\ & \frac{\rho }{2}||Gx-h+\frac{\lambda }{\rho }|{|}^2+\\ & \frac{\rho }{2}||max[Px-q+\frac{\eta }{\rho },0]|{|}^2\end{array}$$$$\begin{array}{rl}\mathrm{\nabla }{\mathcal{L}}_{\rho }(x,\mu ,\nu ,\lambda ,\eta )=& c-\rho \sum _{i=1}^m{A}_i^T{P}_{{\mathcal{K}}_i}(\frac{{\mu }_i}{\rho }-A_{i}x-b_i)+\\ & \rho \sum _{j=1}^q(x^T{J}_j-r_j^T+\frac{{\nu }_j}{\rho })(2J_{j}x-r_j)+\\ & \rho G^T(Gx-h+\frac{\lambda }{\rho })+\\ & \rho P^T\{max[Px-q+\frac{\eta }{\rho },0]\}\end{array}$$

Click me to toggle the code

Topp.hpp

class Topp {
 private:
  static double loss(void* instance, const Eigen::VectorXd& optX,
                    Eigen::VectorXd& optG) {
    Topp* topp = static_cast<Topp*>(instance);
    double res = topp->f.dot(optX);
    optG = topp->f;

    // linear equality constraints
    Eigen::VectorXd resEq = topp->G * optX - topp->h + topp->lambda / topp->rho;
    res += topp->rho / 2 * resEq.squaredNorm() * LINEAR_EQ_COEFF;
    optG += topp->rho * topp->G.transpose() * resEq * LINEAR_EQ_COEFF;

    // linear inequality constraints
    Eigen::VectorXd resIneq = max(topp->P * optX - topp->q + topp->eta / topp->rho, 0);
    res += topp->rho / 2 * resIneq.squaredNorm() * LINEAR_INEQ_COEFF;
    optG += topp->rho * topp->P.transpose() * resIneq * LINEAR_INEQ_COEFF;

    // second order cone constraints
    for (int i = 0; i < topp->n_soc; ++i) {
    Eigen::VectorXd resSoc = socProjection(topp->mus[i] / topp->rho - topp->As[i] * optX - topp->bs[i]);
    res += topp->rho / 2 * resSoc.squaredNorm() * SOC_COEFF;
    optG -= topp->rho * topp->As[i].transpose() * resSoc * SOC_COEFF;
    }

    // quadratic equality constraints
    for (int i = 0; i < topp->n_quadeq; ++i) {
    double resQuadeq = (optX.transpose() * topp->Js[i]).dot(optX) - topp->rs[i].dot(optX) + topp->nus[i] / topp->rho;
    res += topp->rho / 2 * resQuadeq * resQuadeq * QUAD_EQ_COEFF;
    optG += topp->rho * resQuadeq * (2 * topp->Js[i] * optX - topp->rs[i]) * QUAD_EQ_COEFF;
    }

    return res;
  }
};

The projection of a vector to a second order cone is in the Eq. 21 in the report. The corresponding code is shown below.

Eigen::VectorXd socProjection(const Eigen::VectorXd& v) {
  if (v.rows() == 1) {
    return v;
  }
  double v0 = v(0);
  Eigen::VectorXd v1 = v.tail(v.rows() - 1);
  if (v0 > v1.norm()) {
    return v;
  } else if (v0 < -v1.norm()) {
    return Eigen::VectorXd::Zero(v.rows());
  } else {
    Eigen::VectorXd Pk = Eigen::VectorXd::Zero(v.rows());
    Pk(0) = v1.norm();
    Pk.tail(v.rows() - 1) = v1;
    Pk *= (v0 + v1.norm()) / 2 / v1.norm();
    return Pk;
  }
}

Variables Update

The update of the dual variables is shown in the Eq. 32 in the report. The corresponding code is shown below.

$$\begin{array}{rl}x& \leftarrow \arg \underset{x}{min}{\mathcal{L}}_{\rho }(x,\mu ,\nu ,\lambda ,\eta )\\ {\mu }_i& \leftarrow P_{{\mathcal{K}}_i}({\mu }_i-\rho (A_{i}x+b_i))\\ {\nu }_j& \leftarrow {\nu }_j+\rho (x^T{J}_{j}x-r_j^{T}x)\\ \lambda & \leftarrow \lambda +\rho (Gx-h)\\ \eta & \leftarrow max[\eta +\rho (Px-q),0]\\ \rho & \leftarrow min[(1+\gamma )\rho ,\beta ]\end{array}$$

for (int i = 0; i < n_soc; ++i) {
  mus[i] = socProjection(mus[i] - rho * (As[i] * x + bs[i]));
}
for (int i = 0; i < n_quadeq; ++i) {
  nus[i] = nus[i] + rho * (x.transpose() * Js[i] * x - rs[i].dot(x));
}
lambda = lambda + rho * (G * x - h);
eta = max(eta + rho * (P * x - q), 0);
rho = std::min(rho * (1 + GAMMA), BETA);

Reference

Image	Link
	https://mathworld.wolfram.com/images/eps-svg/PolyhedronConvex_1000.svg
	https://www.tandfonline.com/cms/asset/bc9fed8a-15a8-49ee-96be-ce81ead2a54b/tgis_a_1988088_f0001_b.gif
	https://mathworld.wolfram.com/images/eps-svg/CubicSpline_700.svg