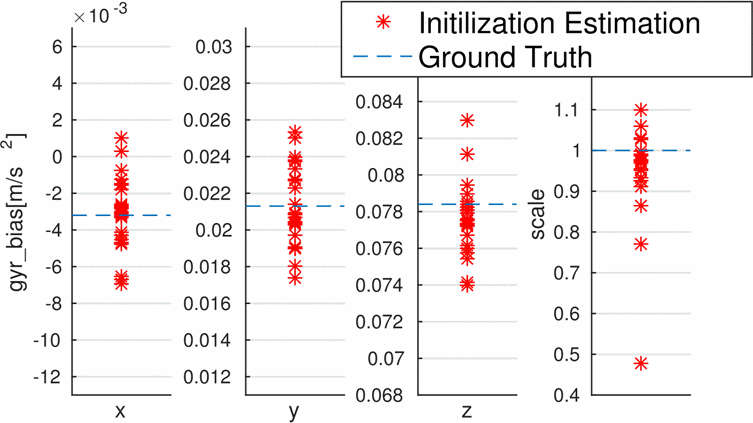
Robust Initialization of VINS

T. Qin and S. Shen, “Robust initialization of monocular visual-inertial estimation on aerial robots,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC: IEEE, Sep. 2017, pp. 4225–4232. doi: 10.1109/IROS.2017.8206284.

利用松耦合的方式对齐 IMU 与视觉

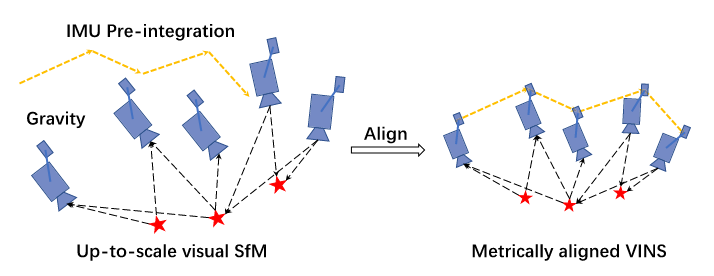
IMU 测量模型有

$$\begin{array}{rl}\hat{\mathit{\omega }}& ={\mathit{\omega }}^b+{\mathbf{b}}^g+{\mathbf{n}}^g\\ \hat{\mathbf{a}}& ={\mathbf{R}}_{bw}({\mathbf{a}}^w+{\mathbf{g}}^w)+{\mathbf{b}}^a+{\mathbf{n}}^a\end{array}$$

预积分

$$\begin{array}{rl}{\mathit{\alpha }}_{b_i{b}_j}& ={\iint }_{t\in [i,j]}{\mathbf{R}}_{b_i{b}_t}({\hat{\mathbf{a}}}^{b_t}-{\mathbf{b}}^a)\mathrm{d}{t}^2\\ {\mathit{\beta }}_{b_i{b}_j}& ={\int }_{t\in [i,j]}{\mathbf{R}}_{b_i{b}_t}({\hat{\mathbf{a}}}^{b_t}-{\mathbf{b}}^a)\mathrm{d}t\\ {\mathbf{q}}_{b_i{b}_j}& ={\int }_{t\in [i,j]}{\mathbf{q}}_{b_i{b}_t}\otimes \left[\begin{array}{c}0\\ \frac{1}{2}({\hat{\mathit{\omega }}}^{b_t}-{\mathbf{b}}^g)\end{array}\right]\mathrm{d}t\end{array}$$

有一阶泰勒展开近似

$$\begin{array}{rl}{\mathit{\alpha }}_{b_i{b}_j}& \approx {\hat{\mathit{\alpha }}}_{b_i{b}_j}+{\mathbf{J}}_{b^a}^{\alpha }\delta {\mathbf{b}}^a+{\mathbf{J}}_{b^g}^{\alpha }\delta {\mathbf{b}}^g\\ {\mathit{\beta }}_{b_i{b}_j}& \approx {\hat{\mathit{\beta }}}_{b_i{b}_j}+{\mathbf{J}}_{b^a}^{\beta }\delta {\mathbf{b}}^a+{\mathbf{J}}_{b^g}^{\beta }\delta {\mathbf{b}}^g\\ {\mathbf{q}}_{b_k{b}_{k+1}}& \approx {\hat{\mathbf{q}}}_{b_k{b}_{k+1}}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{J}}_{b^g}^{\mathbf{q}}\delta {\mathbf{b}}^g\end{array}\right]\end{array}$$

SfM 给出视觉约束，$\overline{·}$ 表示非米制单位

$$\begin{array}{rl}{\mathbf{q}}_{c_0{b}_k}& ={\mathbf{q}}_{c_0{c}_k}\otimes {\mathbf{q}}_{bc}^{-1}\\ s{\overline{\mathbf{p}}}_{c_0{b}_k}& =s{\overline{\mathbf{p}}}_{c_0{c}_k}-{\mathbf{R}}_{c_0{b}_k}{\mathbf{p}}_{bc}\end{array}$$

估计外参数 ${\mathbf{q}}_{bc}$

对于相邻时刻 $k,k+1$ 的 IMU 旋转积分 ${\mathbf{q}}_{b_k{b}_{k+1}}$ 和视觉测量 ${\mathbf{q}}_{c_k{c}_{k+1}}$

$${\mathbf{q}}_{b_k{c}_{k+1}}={\mathbf{q}}_{bc}\otimes {\mathbf{q}}_{c_k{c}_{k+1}}={\mathbf{q}}_{b_k{b}_{k+1}}\otimes {\mathbf{q}}_{bc}$$$$([{\mathbf{q}}_{c_k{c}_{k+1}}{]}_R-[{\mathbf{q}}_{b_k{b}_{k+1}}{]}_L){\mathbf{q}}_{bc}=\mathbf{0}$$

$[·{]}_L,[·{]}_R$ 为四元数的左乘矩阵和右乘矩阵，$[·{]}_{\times }$ 为反对称矩阵

$$\begin{array}{rl}[\mathbf{q}{]}_L& =q_{\omega }\mathbf{I}+\left[\begin{array}{cc}0& -{\mathbf{q}}_v^T\\ {\mathbf{q}}_v& [{\mathbf{q}}_v{]}_{\times }\end{array}\right]\\ [\mathbf{q}{]}_R& =q_{\omega }\mathbf{I}+\left[\begin{array}{cc}0& -{\mathbf{q}}_v^T\\ {\mathbf{q}}_v& -[{\mathbf{q}}_v{]}_{\times }\end{array}\right]\\ [\mathit{\omega }{]}_{\times }& =\left[\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ -{\omega }_y& {\omega }_x& 0\end{array}\right]\end{array}$$

将多个时刻的 IMU 预积分和视觉测量累计，即可得到关于 ${\mathbf{q}}_{bc}$ 的超定方程组

$$\left[\begin{array}{c}[{\mathbf{q}}_{c_0{c}_1}{]}_R-[{\mathbf{q}}_{b_0{b}_1}{]}_L\\ [{\mathbf{q}}_{c_1{c}_2}{]}_R-[{\mathbf{q}}_{b_1{b}_2}{]}_L\\ ⋮\\ [{\mathbf{q}}_{c_n{c}_{n-1}}{]}_R-[{\mathbf{q}}_{b_n{b}_{n-1}}]\end{array}\right]{\mathbf{q}}_{bc}=\mathbf{0}$$

利用奇异值分解可解得 ${\mathbf{q}}_{bc}$

估计陀螺仪偏置

标定得到 ${\mathbf{q}}_{bc}$ 后，利用旋转约束，可估计处陀螺仪偏置

$$\delta {\mathbf{b}}^g=\arg \underset{\delta {\mathbf{b}}^g}{min}\sum _{k\in \mathcal{B}}{\left|\left|{\lfloor {\mathbf{q}}_{c_0{b}_{k+1}}^{-1}\otimes {\mathbf{q}}_{c_0{b}_k}\otimes {\mathbf{q}}_{b_k{b}_{k+1}}\rfloor }_{\text{xyz}}\right|\right|}^2$$

$\mathcal{B}$ 为所有关键帧的集合，其中目标函数取最小值 $0$ 时

$${\mathbf{q}}_{c_0{b}_{k+1}}^{-1}\otimes {\mathbf{q}}_{c_0{b}_k}\otimes {\mathbf{q}}_{b_k{b}_{k+1}}=\left[\begin{array}{c}1\\ \mathbf{0}\end{array}\right]$$

又由旋转预积分一阶泰勒近似

$${\mathbf{q}}_{b_k{b}_{k+1}}\approx {\hat{\mathbf{q}}}_{b_k{b}_{k+1}}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{J}}_{b^g}^{\mathbf{q}}\delta {\mathbf{b}}^g\end{array}\right]$$

联立得到

$$\left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{J}}_{b^g}^{\mathbf{q}}\delta {\mathbf{b}}^g\end{array}\right]={\hat{\mathbf{q}}}_{b_k{b}_{k+1}}^{-1}\otimes {\mathbf{q}}_{c_0{b}_k}^{-1}\otimes {\mathbf{q}}_{c_0{b}_{k+1}}$$

考虑虚部

$${\mathbf{J}}_{b^g}^{\mathbf{q}}\delta {\mathbf{b}}^g=2{\lfloor {\hat{\mathbf{q}}}_{b_k{b}_{k+1}}^{-1}\otimes {\mathbf{q}}_{c_0{b}_k}^{-1}\otimes {\mathbf{q}}_{c_0{b}_{k+1}}\rfloor }_{\text{xyz}}$$

进一步可以构建正定方程组，通过 Cholesky 分解求解 $\delta {\mathbf{b}}^g$

$$({\mathbf{J}}_{b^g}^{\mathbf{q}}{)}^T{\mathbf{J}}_{b^g}^{\mathbf{q}}\delta {\mathbf{b}}^g=2({\mathbf{J}}_{b^g}^{\mathbf{q}}{)}^T{\lfloor {\hat{\mathbf{q}}}_{b_k{b}_{k+1}}^{-1}\otimes {\mathbf{q}}_{c_0{b}_k}^{-1}\otimes {\mathbf{q}}_{c_0{b}_{k+1}}\rfloor }_{\text{xyz}}$$

解得 $\delta {\mathbf{b}}^g$ 后，重新计算预积分项 ${\hat{\mathit{\alpha }}}_{b_k{b}_k+1},{\hat{\mathit{\beta }}}_{b_k{b}_{k+1}},{\hat{\mathbf{q}}}_{b_k{b}_{k+1}}$

初始化速度、重力和尺度因子

所有我们希望估计的变量包括

$${\mathcal{X}}_I={\left[\begin{array}{ccccc}{\mathbf{v}}_0^{b_0}& {\mathbf{v}}_1^{b_1}& \cdots {\mathbf{v}}_n^{b_n}& {\mathbf{g}}^{c_0}& \mathbf{s}\end{array}\right]}^T$$

由 $1.3$ 式和 $2.1$ 式，得到

$$\begin{array}{rl}& {\mathit{\alpha }}_{b_k{b}_{k+1}}={\mathbf{R}}_{b_k{c}_0}(s({\overline{\mathbf{p}}}_{c_0{b}_{k+1}}-{\overline{\mathbf{p}}}_{c_0{b}_k})+\frac{1}{2}{\mathbf{g}}^{c_0}\mathrm{\Delta }{t}_k^2-{\mathbf{R}}_{c_0{b}_k}{\mathbf{v}}_k^{b_k}\mathrm{\Delta }{t}_k)\\ & {\mathit{\beta }}_{b_k{b}_{k+1}}={\mathbf{R}}_{b_k{c}_0}({\mathbf{R}}_{c_0{b}_{k+1}}{\mathbf{v}}_k^{b_k}+{\mathbf{g}}^{c_0}\mathrm{\Delta }{t}_k-{\mathbf{R}}_{c_0{b}_k}{\mathbf{v}}_k^{b_k})\end{array}$$

整理方程得到

$${\hat{\mathbf{z}}}_{b_{k+1}}^{b_k}=\left[\begin{array}{c}{\hat{\mathit{\alpha }}}_{b_k{b}_{k+1}}-{\mathbf{p}}_{bc}+{\mathbf{R}}_{b_k{c}_0}{\mathbf{R}}_{c_0{b}_{k+1}}{\mathbf{p}}_{bc}\\ {\hat{\mathit{\beta }}}_{b_k{b}_{k+1}}\end{array}\right]={\mathbf{H}}^k{\mathcal{X}}_I^k+{\mathbf{n}}^k$$

其中

$$\begin{array}{rl}{\mathcal{X}}_I^k& ={\left[\begin{array}{cccc}{\mathbf{v}}_k^{b_k}& {\mathbf{v}}_{k+1}^{b_{k+1}}& {\mathbf{g}}^{c_0}& s\end{array}\right]}^T\\ {\mathbf{H}}_{b_{k+1}}^{b_k}& =\left[\begin{array}{cccc}-\mathbf{I}\mathrm{\Delta }{t}_k& \mathbf{0}& \frac{1}{2}{\mathbf{R}}_{b_k{c}_0}\mathrm{\Delta }{t}_k^2& {\mathbf{R}}_{b_k{c}_0}({\overline{\mathbf{p}}}_{c_0{b}_{k+1}}-{\overline{\mathbf{p}}}_{c_0{b}_k})\\ -\mathbf{I}& {\mathbf{R}}_{b_k{c}_0}{\mathbf{R}}_{c_0{b}_{k+1}}& {\mathbf{R}}_{b_k{c}_0}\mathrm{\Delta }{t}_k& 0\end{array}\right]\end{array}$$

进而可以转化为最小二乘问题求解

$${\mathcal{X}}_I=\arg \underset{{\mathcal{X}}_I}{min}\sum _{k\in \mathcal{B}}||{\hat{\mathbf{z}}}_{b_{k+1}}^{b_k}-{\mathbf{H}}_{b_{k+1}}^{b_k}{\mathcal{X}}_I^k|{|}^2$$

同样可以通过 Chologky 分解求得

重力向量优化

在重力模长已知的情况下，重力向量实际自由度为 $2$，可以利用球面坐标进行参数化

$${\hat{\mathbf{g}}}^{c_0}=||g||(\frac{{\tilde{\mathbf{g}}}^{c_0}}{||{\tilde{\mathbf{g}}}^{c_0}||}+w_1{\mathbf{b}}_1+w_2{\mathbf{b}}_2)$$

${\tilde{\mathbf{g}}}^{c_0}$ 为 $2.15$ 中求得的重力向量，记 $\frac{{\tilde{\mathbf{g}}}^{c_0}}{||{\tilde{\mathbf{g}}}^{c_0}||}$ 为 ${\widehat{\overline{\mathbf{g}}}}^{c_0}$

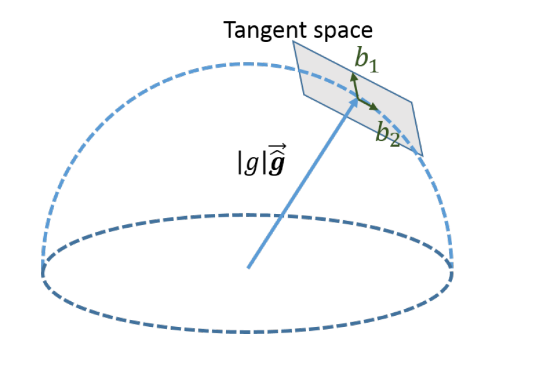
可以通过如下方式找到一组基底垂直于 ${\widehat{\overline{\mathbf{g}}}}^{c_0}$

$$\begin{array}{rl}& {\mathbf{b}}_1=\{\begin{array}{ll}{\widehat{\overline{\mathbf{g}}}}^{c_0}\times [1,0,0{]}^T,& {\widehat{\overline{\mathbf{g}}}}^{c_0}\ne [1,0,0{]}^T\\ {\widehat{\overline{\mathbf{g}}}}^{c_0}\times [0,0,1{]}^T,& \text{otherwise}\end{array}\\ & {\mathbf{b}}_2={\widehat{\overline{\mathbf{g}}}}^{c_0}\times {\mathbf{b}}_1\end{array}$$

将 $2.17$ 式代入 $2.15$ 式，得到

$$\begin{array}{rl}{\mathcal{X}}_I^k& ={\left[\begin{array}{cccc}{\mathbf{v}}_k^{b_k}& {\mathbf{v}}_{k+1}^{b_{k+1}}& {\mathbf{w}}^{c_0}& s\end{array}\right]}^T\\ {\mathbf{H}}_{b_{k+1}}^{b_k}& =\left[\begin{array}{cccc}-\mathbf{I}\mathrm{\Delta }{t}_k& \mathbf{0}& \frac{1}{2}{\mathbf{R}}_{b_k{c}_0}\left[\begin{array}{c}{\mathbf{b}}_1^T\\ {\mathbf{b}}_2^T\end{array}\right]\mathrm{\Delta }{t}_k^2& {\mathbf{R}}_{b_k{c}_0}({\overline{\mathbf{p}}}_{c_0{b}_{k+1}}-{\overline{\mathbf{p}}}_{c_0{b}_k})\\ -\mathbf{I}& {\mathbf{R}}_{b_k{c}_0}{\mathbf{R}}_{c_0{b}_{k+1}}& {\mathbf{R}}_{b_k{c}_0}\left[\begin{array}{c}{\mathbf{b}}_1^T\\ {\mathbf{b}}_2^T\end{array}\right]\mathrm{\Delta }{t}_k& 0\end{array}\right]\end{array}$$

观测方程变为

$${\hat{\mathbf{z}}}_{b_{k+1}}^{b_k}=\left[\begin{array}{c}{\hat{\mathit{\alpha }}}_{b_k{b}_{k+1}}-{\mathbf{p}}_{bc}+{\mathbf{R}}_{b_k{c}_0}{\mathbf{R}}_{c_0{b}_{k+1}}{\mathbf{p}}_{bc}-\frac{1}{2}{\mathbf{R}}_{b_k{c}_0}{\tilde{\mathbf{g}}}^{c_0}\mathrm{\Delta }{t}_k^2\\ {\hat{\mathit{\beta }}}_{b_k{b}_{k+1}}-{\mathbf{R}}_{b_k{c}_0}{\tilde{\mathbf{g}}}^{c_0}\mathrm{\Delta }{t}_k\end{array}\right]$$

利用最小二乘对 ${\mathcal{X}}_I^k$ 进一步优化

视觉惯性对齐

根据旋转的性质和李代数的指数映射，我们可以构建从 $c_0$ 系到 $w$ 系的旋转矩阵 ${\mathbf{R}}_{w{c}_0}$

$${\mathbf{R}}_{w{c}_0}=\exp [\arctan \left(\frac{||{\hat{\mathbf{g}}}^{c_0}\times {\hat{\mathbf{g}}}^w||}{{\hat{\mathbf{g}}}^{c_0}\cdot {\hat{\mathbf{g}}}^w}\right)\cdot \frac{{\hat{\mathbf{g}}}^{c_0}\times {\hat{\mathbf{g}}}^w}{||{\hat{\mathbf{g}}}^{c_0}\times {\hat{\mathbf{g}}}^w||}]$$

接着为所有 $c_0$ 系为坐标系的向量左乘 ${\mathbf{R}}_{w{c}_0}$，同时将非米制的 $\overline{\mathbf{p}}$ 通过尺度因子 $s$ 恢复为 $\mathbf{p}$

未估计的参数

作者通过实验指出二者加速度计偏置 ${\mathbf{b}}^a$ 和相机与 IMU 间的平移向量 ${\mathbf{p}}_{bc}$ 对系统精度影响极小，可以不在初始化中显式优化